
题目列表(包括答案和解析)
一医生知道某种疾病患者的自然痊愈率为![]() ,为实验一种新药是否有效,把它给10个病人服用.他事先决定,若这10个病人中至少有4个治好,则认为这种药有效,提高了痊愈率.否则认为无效.求
,为实验一种新药是否有效,把它给10个病人服用.他事先决定,若这10个病人中至少有4个治好,则认为这种药有效,提高了痊愈率.否则认为无效.求
(1)虽然新药有效,并把痊愈率提高到了![]() ,但通过实验却被否定的概率;
,但通过实验却被否定的概率;
(2)新药完全无效,但通过实验却被判断为有效的概率.
参考数据:
p | 2.0000 | 3.0000 | 4.0000 | 5.0000 | 6.0000 | 7.0000 | 8.0000 | 9.0000 | 10.0000 |
0.2500 | 0.0625 | 0.0156 | 0.0039 | 0.0010 | 0.0002 | 0.0001 | 0.0000 | 0.0000 | 0.0000 |
0.3500 | 0.1225 | 0.0429 | 0.0150 | 0.0053 | 0.0018 | 0.0006 | 0.0002 | 0.0001 | 0.0000 |
0.6500 | 0.4225 | 0.2746 | 0.1785 | 0.1160 | 0.0754 | 0.0490 | 0.0319 | 0.0207 | 0.0135 |
0.7500 | 0.5625 | 0.4219 | 0.3164 | 0.2373 | 0.1780 | 0.1335 | 0.1001 | 0.0751 | 0.0563 |
答案请保留四位有效数字.
先阅读理解下面的例题,再按要求解答:
例题:解一元二次不等式![]() .
.
解:∵![]() ,
,
∴![]() .
.
由有理数的乘法法则“两数相乘,同号得正”,有
(1)![]() (2)
(2)![]()
解不等式组(1),得![]() ,
,
解不等式组(2),得![]() ,
,
故![]() 的解集为
的解集为![]() 或
或![]() ,
,
即一元二次不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
问题:求分式不等式![]() 的解集.
的解集.
数列 首项
首项 ,前
,前 项和
项和 满足等式
满足等式 (常数
(常数 ,
, ……)
……)
(1)求证: 为等比数列;
为等比数列;
(2)设数列 的公比为
的公比为 ,作数列
,作数列 使
使 (
( ……),求数列
……),求数列 的通项公式.
的通项公式.
(3)设 ,求数列
,求数列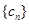 的前
的前 项和
项和 .
.
【解析】第一问利用由 得
得
两式相减得
故 时,
时,
从而 又
又 即
即 ,而
,而
从而 故
故
第二问中,
 又
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为
第三问中,
 两边同乘以
两边同乘以
利用错位相减法得到和。
(1)由 得
得
两式相减得
故 时,
时,
从而 ………………3分
………………3分
又 即
即 ,而
,而
从而 故
故
 对任意
对任意 ,
, 为常数,即
为常数,即 为等比数列………………5分
为等比数列………………5分
(2)
 ……………………7分
……………………7分
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为 ………………9分
………………9分
(3)
 两边同乘以
两边同乘以
 ………………11分
………………11分
两式相减得

在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
【解析】本试题主要考查了古典概型概率的求解。第一问中,基本事件数为共有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
总数为16种.其中取出的两个小球上标号为相邻整数的基本事件有:
(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)共6种利用古典概型可知,P=3 /8 ;
(2)其中取出的两个小球上标号之和能被3整除的基本事件有:
(1,2),(2,1),(2,4),(3,3),(4,2)共5种可得概率值5 /16 ;
解:甲、乙两个盒子里各取出1个小球计为(X,Y)则基本事件
共有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
总数为16种.
(1)其中取出的两个小球上标号为相邻整数的基本事件有:
(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)共6种
故取出的两个小球上标号为相邻整数的概率P=3 /8 ;
(2)其中取出的两个小球上标号之和能被3整除的基本事件有:
(1,2),(2,1),(2,4),(3,3),(4,2)共5种
故取出的两个小球上标号之和能被3整除的概率为5 /16 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com