
题目列表(包括答案和解析)
(1)他们每人都至少解出1题;
(2)在没有解出第1题的那些学生中,解出第2题的是解出第3题的人数的2倍;
(3)只解出第1题的比余下的学生中解出第1题的多1人;
(4)只解出1道题的学生中,有一半没有解出第1题.
试问有多少学生只解出第2题?
从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:

⑴80~90这一组的频数、频率分别是多少?
⑵估计这次环保知识竞赛的及格率(60分及以上为及格). (本小题满分10分)
【解析】本试题主要考查了统计和概率的综合运用。
第一问频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
第二问0.015×10+0.025×10+0.03×10+0.005×10=0.75
解:(1)频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
(2)0.015×10+0.025×10+0.03×10+0.005×10=0.75
已知函数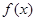 =
= .
.
(Ⅰ)当 时,求不等式
时,求不等式
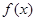 ≥3的解集;
≥3的解集;
(Ⅱ) 若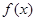 ≤
≤ 的解集包含
的解集包含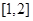 ,求
,求 的取值范围.
的取值范围.
【命题意图】本题主要考查含绝对值不等式的解法,是简单题.
【解析】(Ⅰ)当 时,
时,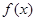 =
=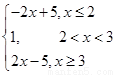 ,
,
当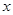 ≤2时,由
≤2时,由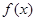 ≥3得
≥3得 ,解得
,解得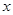 ≤1;
≤1;
当2<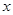 <3时,
<3时,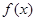 ≥3,无解;
≥3,无解;
当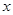 ≥3时,由
≥3时,由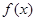 ≥3得
≥3得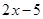 ≥3,解得
≥3,解得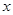 ≥8,
≥8,
∴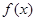 ≥3的解集为{
≥3的解集为{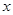 |
|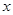 ≤1或
≤1或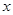 ≥8};
≥8};
(Ⅱ) 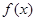 ≤
≤

 ,
,
当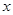 ∈[1,2]时,
∈[1,2]时, =
= =2,
=2,
∴ ,有条件得
,有条件得 且
且 ,即
,即 ,
,
故满足条件的 的取值范围为[-3,0]
的取值范围为[-3,0]
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| x2+y2 |
| b |
| 3 |
| 25 |
| 4 |
| 25 |
| 1 |
| 25 |
| 1 |
| 14 |
| 1 |
| 14 |
例10.(2004年重庆卷)某工厂生产某种产品,已知该产品的月生产量(吨)与每吨产品的价格(元/吨)之间的关系式为:,且生产x吨的成本为(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
解:每月生产x吨时的利润为
,故它就是最大值点,且最大值为:
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com