
题目列表(包括答案和解析)
| 甲 | 乙 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,分别测出它们的高度如下(单位:cm)
甲:19 20 21 23 25 29 32 33 37 41
乙:10 26 30 30 34 37 44 46 46 47
| 甲 | 乙 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
(1)用茎叶图表示上述两组数据,并对两块地抽取树苗的高度的平均数和中位数进行比较,写出两个统计结论;
(2)现苗圃基地将甲、乙两块地的树苗合在一起,按高度分成一、二两个等级,每个等级按不同的价格出售.某市绿化部门下属的2个单位计划购买甲、乙两地种植的树苗.已知每个单位购买每个等级树苗所需费用均为5万元,且每个单位对每个等级树苗买和不买的可能性各占一半,求该市绿化部门此次采购所需资金总额X的分布列及数学期望值E(X).
现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.
【解析】依题意,这4个人中,每个人去参加甲游戏的概率为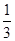 ,去参加乙游戏的概率为
,去参加乙游戏的概率为 .
.
设“这4个人中恰有i人去参加甲游戏”为事件

则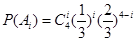 .
.
(1)这4个人中恰有2人去参加甲游戏的概率
(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则 .由于
.由于 互斥,故
互斥,故
所以,这个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为 .
.
(3) 的所有可能取值为0,2,4.由于
的所有可能取值为0,2,4.由于 互斥,
互斥, 互斥,故
互斥,故
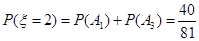

所以 的分布列是
的分布列是
|
|
0 |
2 |
4 |
|
P |
|
|
|
随机变量 的数学期望
的数学期望 .
.
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
【解析】本试题主要考查了古典概型概率的求解。第一问中,基本事件数为共有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
总数为16种.其中取出的两个小球上标号为相邻整数的基本事件有:
(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)共6种利用古典概型可知,P=3 /8 ;
(2)其中取出的两个小球上标号之和能被3整除的基本事件有:
(1,2),(2,1),(2,4),(3,3),(4,2)共5种可得概率值5 /16 ;
解:甲、乙两个盒子里各取出1个小球计为(X,Y)则基本事件
共有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
总数为16种.
(1)其中取出的两个小球上标号为相邻整数的基本事件有:
(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)共6种
故取出的两个小球上标号为相邻整数的概率P=3 /8 ;
(2)其中取出的两个小球上标号之和能被3整除的基本事件有:
(1,2),(2,1),(2,4),(3,3),(4,2)共5种
故取出的两个小球上标号之和能被3整除的概率为5 /16 ;
例10.(2004年重庆卷)某工厂生产某种产品,已知该产品的月生产量(吨)与每吨产品的价格(元/吨)之间的关系式为:,且生产x吨的成本为(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
解:每月生产x吨时的利润为
,故它就是最大值点,且最大值为:
答:每月生产200吨产品时利润达到最大,最大利润为315万元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com