
题目列表(包括答案和解析)
相距![]() 的虚线MP、NQ间有水平向右的匀强电场,将质量为
的虚线MP、NQ间有水平向右的匀强电场,将质量为![]() 、电荷量
、电荷量![]() 的带电小球F从两极板上方O点以
的带电小球F从两极板上方O点以![]() 的初速度水平抛出,O点距离电场上端的高度
的初速度水平抛出,O点距离电场上端的高度![]() ,小球恰好从电场上边缘M处进入电场,并沿直线运动。有一与虚线 MP、NQ垂直的光滑绝缘的水平台面,上面有用长为
,小球恰好从电场上边缘M处进入电场,并沿直线运动。有一与虚线 MP、NQ垂直的光滑绝缘的水平台面,上面有用长为![]() 的绝缘轻杆连接的两个质量均为
的绝缘轻杆连接的两个质量均为![]() 的带电小球A和B组成的带电系统,A球的带电量为
的带电小球A和B组成的带电系统,A球的带电量为![]() ,B球的带电量为
,B球的带电量为![]() 。如图所示,初始A和B分别静止于虚线MP的两侧,且到MP的距离相同,若视小球为质点,不计轻杆的质量,g取10 m/s2,求:
。如图所示,初始A和B分别静止于虚线MP的两侧,且到MP的距离相同,若视小球为质点,不计轻杆的质量,g取10 m/s2,求:
 (1)两极板间的电场强度;
(1)两极板间的电场强度;
(2)B球刚进入电场时,带电系统的速度大小;
(3)带电系统在电场中运动的周期。
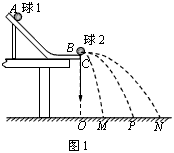
用半径相同的小球1和小球2的碰撞验证动量守恒定律,实验装置如图10所示,斜槽与水平槽圆滑连接。安装好实验装置,在地上铺一张白纸,白纸上铺放复写纸,记下重锤线所指的位置O。接下来的实验步骤如下:
步骤1:不放小球2,让小球1从斜槽上A点由静止滚下,并落在地面上。重复多次,用尽可能小的圆,把小球的所有落点圈在里面,认为其圆心就是小球落点的平均位置;
步骤2:把小球2放在斜槽前端边缘处的C点,让小球1从A点由静止滚下,使它们碰撞。重复多次,并使用与步骤1同样的方法分别标出碰撞后两小球落点的平均位置;
步骤3:用刻度尺分别测量三个落地点的平均位置M、P、N离O点的距离,即线段OM、OP、ON的长度。
①在上述实验操作中,下列说法正确的是___________
A.小球1的质量一定大于球2的质量,小球1的半径可以大于小球2的半径
B.将小球静止放置在轨道末端看小球是否滚动来检测斜槽轨道末端是否水平
C.小球在斜槽上的释放点应该越高越好,可样碰前的速度大,测量误差会小
D.复写纸铺在白纸的上面,实验过程中复写纸可以随时拿起看印迹是否清晰并进行移动
②以下提供的器材中,本实验必需的有( )
A.刻度尺 B.游标卡尺 C.天平 D.秒表
③设球1的质量为m1,球2的质量为m2,MP的长度为l1,ON的长度为l2,则本实验验证动量守恒定律的表达式为________________________,即说明两球碰撞遵守动量守恒定律。
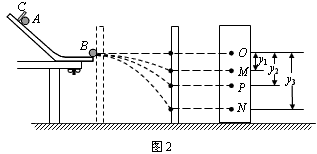
④完成实验后,实验小组对上述装置进行了如图11所示的改变:(I)在木板表面先后钉上白纸和复写纸,并将木板竖直立于靠近槽口处,使小球A从斜槽轨道上某固定点C由静止释放,撞到木板并在白纸上留下痕迹O;(II)将木板向右平移适当的距离固定,再使小球A从原固定点C由静止释放,撞到木板上得到痕迹P;(III)把半径相同的小球B 静止放在斜槽轨道水平段的最右端,让小球A仍从原固定点由静止开始滚下, 与小球B 相碰后,两球撞在木板上得到痕迹 M和 N;(IV)用刻度尺测量纸上O点到M、P、N 三点的距离分别为y1、y2、y3。请你写出用直接测量的物理量来验证两球碰撞过程中动量守恒的表达式: 。(小球A、B的质量分别为m1、m2)

 |
一、1、C2、C 3、B 4、C 5、BC 6、B 7、AD 8、D
二、实验题:(18分)将答案填在题目的空白处,或者要画图连线。
9、(6分)__BE_ (3分) ____AD___(3分)
10、(12分)(1)如图b(4分)
(2)由于RL2比RL1小得多,灯泡L2分得的电压很小,虽然有电流渡过,但功率很小,不能发光。(4分)
(3)如图c
解析:由于灯泡L2和L1额定电压相同,灯泡L2功率大得多,故RL2比RL1小得多,灯泡L2分得的电压很小,虽然有电流渡过,但功率很小,不能发光。(4分)
三、本大题共三小题共计54分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题.答案中必须明确写出数值和单位
11、(16分)(1) 根据带电小球A恰能做完整的圆周运动,因 ,则小球能通过复合场中的最高点P(如图)设经过轨道上的P点的速度为v,由小球A的重力和电场力的合力提供向心力有:
,则小球能通过复合场中的最高点P(如图)设经过轨道上的P点的速度为v,由小球A的重力和电场力的合力提供向心力有:
在圆周轨道的最低点弹簧将B、A两球向左、右弹开,设弹开时A、B两球的速度大小分别为vA、vB,由动量守恒有:
小球A从圆周轨道的最低点运动到P的过程中,由动能定理有:
(2)设BC碰后速度为v1 , B与C碰撞动量守恒
BC整体减速,D球加速,当两者速度相等时设为v2,弹簧最短,弹性势能最大
12、(18分)(1)(6分)设球到D点时的速度为 ,从释放至D点,
,从释放至D点,
根据动能定理 (3分)
(3分)
对 球,根据动量守恒定律
球,根据动量守恒定律  (2分)
(2分)
解得 (1分)
(1分)
(2)(6分)两球进入复合场后,由计算可知 两球在洛伦兹力作用下做匀速圆周运动,轨迹示意图如右图所示(1分)
两球在洛伦兹力作用下做匀速圆周运动,轨迹示意图如右图所示(1分)
 洛伦兹力提供向心力
洛伦兹力提供向心力 (2分)
(2分)
由图可知 (2分)
(2分)
解得 (1分)
(1分)
(3)(6分) 系统损失的机械能
系统损失的机械能

或
解得
13、(20分)⑴设匀速直线运动的速度为v0, ef有效切割长度为l,则电流:
 ,由于v0不变,所以I不变。或由平衡条件证明同样给分(4分)
,由于v0不变,所以I不变。或由平衡条件证明同样给分(4分)
⑵由能量守恒,得:… ………………………(2分)
………………………(2分)
设弹簧形变量为x,由平衡条件,得: 2BIxtan30°= kx…………(2分)
解得 v0 = (2分) k = …(2分)
⑶ef越过O点后,与弹簧脱离,设导体棒最终停止位置距O点的距离为x0,某时刻回路中ef有效切割长度为L1,ef的速度为v,加速度为a,电流为I, 据牛顿第二定律,得:― BIL1= ma
电流 I = = 得: ― = ma……………………… (3分)
取一小段时间△t,速度微小变化为△v,回路面积微小增加为△S,则 ― △t = ma△t
即: ― ∑△t = ∑ma△t ―∑L1v△t = m∑a△t ―∑△S = m∑△v
― x02tan300= 0-mv0 (3分) 将 v0= 代入,得:x 0 = ―― (2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com