
题目列表(包括答案和解析)
(本小题满分12分)等差数列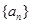 中,
中,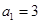 ,前
,前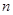 项和为
项和为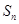 ,等比数列
,等比数列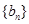 各项均为正数,
各项均为正数, ,且
,且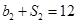 ,
,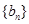 的公比
的公比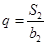
(1)求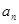 与
与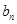 ;
;
(2)求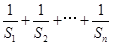
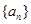 中,
中,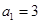 ,前
,前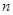 项和为
项和为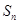 ,等比数列
,等比数列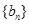 各项均为正数,
各项均为正数,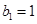 ,且
,且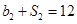 ,
,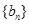 的公比
的公比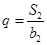
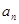 与
与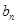 ;
;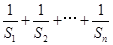
(本小题满分12分)
等差数列![]() 的各项均为整数,
的各项均为整数,![]() ,前
,前![]() n项和为Sn,其中
n项和为Sn,其中![]() 。又等比数列
。又等比数列![]() 中,b1=1,b2S2=64。
中,b1=1,b2S2=64。
(1)求![]() 与
与![]()
(2)证明:![]()
(本小题满分12分)
等差数列![]() 的各项均为正数,
的各项均为正数,![]() ,前
,前![]() 项和为
项和为![]() . 等比数列
. 等比数列![]() 中,
中,![]() ,且
,且![]()
![]() .
.
(Ⅰ)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(Ⅱ)求![]() .
.
(本小题满分12分)
等差数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 各项均为正数,
各项均为正数,![]() ,且
,且![]() ,
,![]() 的公比
的公比![]() .
.
(1)求![]() 与
与![]() ;
;
(2)证明:![]()
一. 选择题:本大题共12小题,每小题5分,共60分。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
D
B
A
A
D
C
D
A
C
C
B
1..因所以对应的点在第四象限,
2..因,
3..令,则,
4..
5. . ,,…,
6.D. 函数
7. .由题知,垂足的轨迹为以焦距为直径的圆,则
又,所以
8.. 常数项为
9. A.
10.. 解:①③④正确,②错误。易求得、到球心的距离分别为3、2,若两弦交于,则⊥,中,有,矛盾。当、、共线时分别取最大值5最小值1。
11. . 一天显示的时间总共有种,和为23总共有4种,故所求概率为.
12.. 解:当时,显然不成立
当时,因当即时结论显然成立;
当时只要即可
即
则
二. 填空题:本大题共4小题,每小题4分,共16分。
13. 14. 15. 16. B、D
13. 由已知得,则
14.
15.
16. 解:真命题的代号是: BD 。易知所盛水的容积为容器容量的一半,故D正确,于是A错误;水平放置时由容器形状的对称性知水面经过点P,故B正确;C的错误可由图1中容器位置向右边倾斜一些可推知点P将露出水面。
三. 解答题:本大题共6小题,共74分。
17.解:由得
∴ ∴
∴,又
∴
由得
即 ∴
由正弦定理得
18.解:(1)的所有取值为
的所有取值为,
、的分布列分别为:
0.8
0.9
1.0
1.125
1.25
P
0.2
0.15
0.35
0.15
0.15
0.8
0.96
1.0
1.2
1.44
P
0.3
0.2
0.18
0.24
0.08
(2)令A、B分别表示方案一、方案二两年后柑桔产量超过灾前产量这一事件,
,
可见,方案二两年后柑桔产量超过灾前产量的概率更大
(3)令表示方案所带来的效益,则
10
15
20
P
0.35
0.35
0.3
10
15
20
P
0.5
0.18
0.32
所以
可见,方案一所带来的平均效益更大。
19.解:(1)设的公差为,的公比为,则为正整数,
,
依题意有①
由知为正有理数,故为的因子之一,
解①得
故
(2)
∴
20.解 :(1)证明:依题设,是的中位线,所以∥,
则∥平面,所以∥。
又是的中点,所以⊥,则⊥。
因为⊥,⊥,
所以⊥面,则⊥,
因此⊥面。
(2)作⊥于,连。因为⊥平面,
根据三垂线定理知,⊥,
就是二面角的平面角。
作⊥于,则∥,则是的中点,则。
设,由得,,解得,
在中,,则,。
所以,故二面角为。
解法二:(1)以直线分别为轴,建立空间直角坐标系,则
所以
所以
所以平面
由∥得∥,故:平面
(2)由已知设
由与共线得:存在有得
同理:
设是平面的一个法向量,
则令得
又是平面的一个法量
所以二面角的大小为
(3)由(2)知,,,平面的一个法向量为。
则。
则点到平面的距离为
21.证明:(1)设,由已知得到,且,,
从而,解得
因此的方程为:
同理的方程为:
又在上,所以,
即点都在直线上
又也在直线上,所以三点共线
(2)垂线的方程为:,
由得垂足,
设重心
所以 解得
由 可得即为重心所在曲线方程
22.解:、当时,,求得 ,
于是当时,;而当 时,.
即在中单调递增,而在中单调递减.
(2).对任意给定的,,由 ,
若令 ,则 … ① ,而 … ②
(一)、先证;因为,,,
又由 ,得 .
所以
.
(二)、再证;由①、②式中关于的对称性,不妨设.则
(?)、当,则,所以,因为 ,
,此时.
(?)、当 …③,由①得 ,,,
因为 所以 … ④
同理得 … ⑤ ,于是 … ⑥
今证明 … ⑦, 因为 ,
只要证 ,即 ,也即 ,据③,此为显然.
因此⑦得证.故由⑥得 .
综上所述,对任何正数,皆有.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com