
题目列表(包括答案和解析)

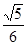 时,求PE及DH的长。
时,求PE及DH的长。如图,在梯形ABCD中, AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan∠ADC=2.
⑴求证:DC=BC;
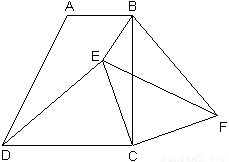
⑵E是梯形内的一点,F是梯形外的一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;⑶在⑵的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.
如图,在梯形ABCD中, AB∥DC,∠BCD=90°,且AB=1,BC=2,
tan∠ADC=2.
⑴求证:DC=BC;
⑵E是梯形内的一点,F是梯形外的一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;⑶在⑵的条件下,当BE:CE=1:2,∠BEC=135°时,求sin∠BFE的值.

| ||
| 6 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com