练习册

  • 练习册
  • 试题
    =8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4???????????????????????????????? 12分 ⑴证明:平面和平面互相垂直;⑵证明:截面和截面面积之和是定值,并求出这个值;⑶若与平面所成的角为,求与平面所成角的正弦值.说明:本小题主要考查空间中的线面关系.面面关系.解三角形等基础知识.考查空间想象能力与逻辑思维能力.满分12分．解法一:(Ⅰ)证明:在正方体中...又由已知可得 所以..所以平面．所以平面和平面互相垂直．???????????????????????? 4分知.又截面PQEF和截面PQGH都是矩形.且PQ=1.所以截面PQEF和截面PQGH面积之和是.是定值．?????????????????????????????????????????????????????????????????????? 8分(III)解:连结BC′交EQ于点M．因为..所以平面和平面PQGH互相平行.因此与平面PQGH所成角与与平面所成角相等．与(Ⅰ)同理可证EQ⊥平面PQGH.可知EM⊥平面.因此EM与的比值就是所求的正弦值．设交PF于点N.连结EN.由知．因为⊥平面PQEF.又已知与平面PQEF成角.所以.即.解得.可知E为BC中点．所以EM=.又.故与平面PQCH所成角的正弦值为．????????????????????????????????????????????????? 12分解法二:以D为原点.射线DA.DC.DD′分别为x.y.z轴的正半轴建立如图的空间直角坐标系D-xyz由已知得.故 .....．(Ⅰ)证明:在所建立的坐标系中.可得..．因为.所以是平面PQEF的法向量．因为.所以是平面PQGH的法向量．因为.所以.所以平面PQEF和平面PQGH互相垂直．????????????????????????????????????????????????????????????????????? 4分(Ⅱ)证明:因为.所以.又.所以PQEF为矩形.同理PQGH为矩形．在所建立的坐标系中可求得..所以.又.所以截面PQEF和截面PQGH面积之和为.是定值．????????????????????????????????????????????? 8分(Ⅲ)解:由已知得与成角.又可得 .即.解得．所以.又.所以与平面PQGH所成角的正弦值为．????????????????????????????????????????????????????????????????????????? 12分 【查看更多】

     

    题目列表(包括答案和解析)

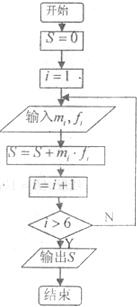    “世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”．为提高公众对健康睡眠的科学认识和自我管理能力，某网站于3月13日起进行了为期一周的在线调查，共有200人参与．现将数据整理分组如表所示．
    （1）画出频率分布直方图；
    （2）调查对象中睡眠时间少于8的频率是多少？
    （3）为了对数据进行分析，采用了计算机辅助计算，算法流程如图所示．求输出的S的值，并说明S的统计意义．
    序号i 分组睡眠时间（小时） 组中值（m1） 频数（人数） 频率（f1）
    1 [4，5） 4.5 8 0.04
    2 [5，6） 5.5 52 0.26
    3 [6，7） 6.5 60 0.30
    4 [7，8） 7.5 56 0.28
    5 [8，9） 8.5 20 0.10
    6 [9，10） 9.5 4 0.02

    查看答案和解析>>

    “世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识，为此某网站进行了持续一周的在线调查，共有200人参加调查，现将数据整理分组如题中表格所示．
    序号（i） 分组睡眠时间 组中值（mi） 频数
    （人数）    		 频率
    （fi）
    1 [4，5） 4.5 8 0.04
    2 [5，6） 5.5 52 0.26
    3 [6，7） 6.5 60 0.30
    4 [7，8） 7.5 56 0.28
    5 [8，9） 8.5 20 0.10
    6 [9，10] 9.5 4 0.02

    （1）在答题卡给定的坐标系中画出频率分布直方图；
    （2）睡眠时间小于8的概率是多少？
    （3）为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图（如图2），求输出的S的值，并说明S的统计意义．

    查看答案和解析>>

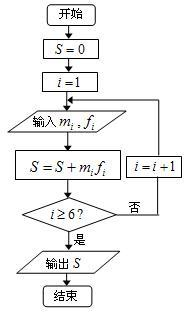    “世界睡眠日”定在每年的3月21日．2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识．为此某网站2009年3月13日到3月20日持续一周的在线调查，共有200人参加调查，现将数据整理分组如题中表格所示．为了对数据进行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图，则输出的S值为
    6
    6
    ，S的统计意义是
    70
    70
    ．
    序号
    （i）    		 分组
    睡眠时间    		 组中值
    （mi）    		 频数
    （人数）    		 频率
    （fi）
    1 [4，5） 4.5 8 0.04
    2 [5，6） 5.5 52 0.26
    3 [6，7） 6.5 60 0.30
    4 [7，8） 7.5 56 0.28
    5 [8，9） 8.5 20 0.10
    6 [9，10] 9.5 4 0.02

    查看答案和解析>>

    国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：

    序号()

    每天睡眠时间

    （小时）

    组中值()

    频数

    频率

    ()

    1

    [4，5)

    4.5

    8

    0.04

    2

    [5，6)

    5.5

    52

    0.26

    3

    [6，7)

    6.5

    60

    0.30

    4

    [7，8)

    7.5

    56

    0.28

    5

    [8，9)

    8.5

    20

    0.10

    6

    [9，10)

    9.5

    4

    0.02

     


    （Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；

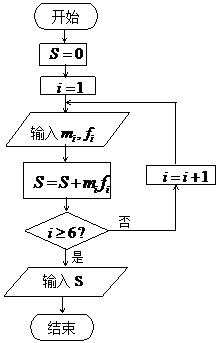
    （Ⅱ）该网站利用上面的算法流程图，对样本数据作进一步统计

    分析，求输出的S的值，并说明S的统计意义.

    查看答案和解析>>

    (本小题满分12分)

    国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：

    序号()

    每天睡眠时间

    （小时）

    组中值()

    频数

    频率

    ()

    1

    [4，5)

    4.5

    8

    0.04

    2

    [5，6)

    5.5

    52

    0.26

    3

    [6，7)

    6.5

    60

    0.30

    4

    [7，8)

    7.5

    56

    0.28

    5

    [8，9)

    8.5

    20

    0.10

    6

    [9，10)

    9.5

    4

    0.02

    （Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；

    （Ⅱ）该网站利用右边的算法流程图，对样本数据作进一步统计分析，求输出的S的值，并说明S的统计意义.

     


    查看答案和解析>>


    同步练习册答案