练习册

  • 练习册
  • 试题
    18．(注意:在试题卷上作答无效)四棱锥中.底面为矩形.侧面底面...．(Ⅰ)证明:,(Ⅱ)设与平面所成的角为.求二面角的大小． 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）

    （注意：在试题卷上作答无效）

    四棱锥中，底面为矩形，侧面底面，，，。

    （Ⅰ）证明：；

    （Ⅱ）设侧面为等边三角形，求二面角的大小。

    查看答案和解析>>

    （本小题满分12分）

    （注意：在试题卷上作答无效）

    已知5只动物中有1只患有某种疾病，需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物，呈阴性即没患病.下面是两种化验方案：

    方案甲：逐个化验，直到能确定患病动物为止；

    方案乙：先任取3只，将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只，然后再逐个化验，直到能确定患病动物为止；若结果呈阴性则在另外2只中任取1只化验。

    求依方案甲所需化验次数不少于依方案乙所需化验次数的概率。

    查看答案和解析>>

    （本小题满分12分）（注意：在试题卷上作答无效）

    “上海世博会”将于2010年5月1日至10月31日在上海举行。世博会“中国馆·贵宾厅”作为接待中外贵宾的重要场所，陈列其中的艺术品是体现兼容并蓄、海纳百川的重要文化载体，为此，上海世博会事物协调局将举办“中国2010年上海世博会‘中国馆·贵宾厅’艺术品方案征集”活动。某地美术馆从馆藏的中国画、书法、油画、陶艺作品中各选一件代表作参与应征，假设代表作中中国画、书法、油画入选“中国馆·贵宾厅”的概率均为，陶艺入选“中国馆·贵宾厅”的概率为” 

    （Ⅰ）求该地美术馆选送的四件代表作中恰有一件作品入选“中国馆·贵宾厅”的概率。

    （Ⅱ）求该地美术馆选送的四件代表作中至多有两件作品入选“中国馆·贵宾厅”的概率

    查看答案和解析>>

    （本小题满分12分）（注意：在试题卷上作答无效）

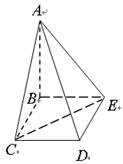
    如图，直角△BCD所在的平面垂直于正△ABC所在的平面，PA⊥平面ABC，,为DB的中点，

    （Ⅰ）证明：AE⊥BC；

    （Ⅱ）线段BC上是否存在一点F使得PF与面DBC所成的角为，若存在，试确定点F的位置，若不存在，说明理由.

    查看答案和解析>>

    （本小题满分12分）（注意：在试题卷上作答无效）

    已知数列的前项和为，且满足

    （Ⅰ）求数列的通项公式；

    （Ⅱ）设求为数列的前项和。

    查看答案和解析>>

     

    1. C.      由

    2. A．     根据汽车加速行驶，匀速行驶，减速行驶结合函数图像可知；

    3. A.       由，，；

    4. D.              ；

    5. C.      由；

    6. B.              由；

    7.D.        由；

    8.A.        只需将函数的图像向左平移个单位得到函数的图像.

    9.D．由奇函数可知，而，则，当时，；当时，，又在上为增函数，则奇函数在上为增函数，.

    10.D．由题意知直线与圆有交点，则.

    另解：设向量，由题意知

    由可得

    11.C．由题意知三棱锥为正四面体，设棱长为，则，棱柱的高（即点到底面的距离），故与底面所成角的正弦值为.

    另解：设为空间向量的一组基底，的两两间的夹角为

    长度均为，平面的法向量为,

    则与底面所成角的正弦值为.

    12.B.分三类：种两种花有种种法；种三种花有种种法；种四种花有种种法.共有.

    13.答案：9．如图，作出可行域，

    作出直线，将平移至过点处

    时，函数有最大值9.

    14. 答案：2.由抛物线的焦点坐标为

    为坐标原点得，，则

    与坐标轴的交点为，则以这三点围成的三角形的面积为

    15.答案：.设，则

    16.答案：.设，作

    ，则，为二面角的平面角

    ，结合等边三角形

    与正方形可知此四棱锥为正四棱锥，则

    ,

    故所成角的余弦值

     

    则点,

    ,

    则,

    故所成角的余弦值.

    17.解析：（Ⅰ）在中，由正弦定理及

    可得

    即，则；

    （Ⅱ）由得

    当且仅当时，等号成立，

    18．解：（1）取中点，连接交于点，

    ，，

    又面面，面，

    ．

    ，

    ，，即，

    面，．

    （2）在面内过点作的垂线，垂足为．

    ，，面，，

    则即为所求二面角的平面角．

    ，，，

    ，则，

    ，即二面角的大小．

    19. 解：（1）求导：

    当时，，，在上递增

    当，求得两根为

    即在递增，递减，

    递增

    （2），且解得：

     20．解：（Ⅰ）解：设、分别表示依方案甲需化验1次、2次。

       、表示依方案乙需化验2次、3次；

       表示依方案甲所需化验次数不少于依方案乙所需化验次数。

      依题意知与独立，且

    ∴

    （Ⅱ）的可能取值为2，3。

    ；

    ∴

    ∴（次）

     

    21. 解：（Ⅰ）设，，

    由勾股定理可得：

    得：，，

    由倍角公式，解得,则离心率．

    （Ⅱ）过直线方程为,与双曲线方程联立

    将，代入，化简有

    将数值代入，有,解得

    故所求的双曲线方程为。

    22. 解析：

    （Ⅰ）证明：，

    故函数在区间(0,1)上是增函数；

    （Ⅱ）证明：（用数学归纳法）（i）当n=1时，，，

    由函数在区间是增函数，且函数在处连续，则在区间是增函数，，即成立；

    （?）假设当时，成立，即

    那么当时，由在区间是增函数，得

    .而，则，

    ，也就是说当时，也成立；

    根据（?）、（?）可得对任意的正整数，恒成立.

     （Ⅲ）证明：由．可得

    1， 若存在某满足，则由⑵知：

    2， 若对任意都有，则

    ，即成立.

     

     

     

     

     

     


    同步练习册答案