
题目列表(包括答案和解析)
已知函数 .
.
(1)若 ,求证:当
,求证:当 时,
时,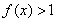 ;
;
(2)若 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围;
(3)求证: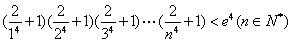 .
.
设等比数列{![]() }的前
}的前![]() 项和
项和![]() ,首项
,首项![]() ,公比
,公比![]() .
.
(1)证明:![]() ;
;
(2)若数列{![]() }满足
}满足![]() ,
,![]() ,求数列{
,求数列{![]() }的通项公式;
}的通项公式;
(3)若![]() ,记
,记![]() ,数列{
,数列{![]() }的前项和为
}的前项和为![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
(本小题满分14分)
已知数列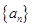 满足:
满足: (其中常数
(其中常数 ).
).
(Ⅰ)求数列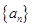 的通项公式;
的通项公式;
(Ⅱ)求证:当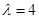 时,数列
时,数列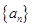 中的任何三项都不可能成等比数列;
中的任何三项都不可能成等比数列;
(Ⅲ)设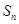 为数列
为数列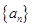 的前
的前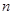 项和.求证:若任意
项和.求证:若任意 ,
,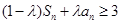
已知函数 ,(
,(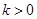 )在
)在 处取得最小值.
处取得最小值.
(Ⅰ)求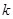 的值;
的值;
(Ⅱ)若 在
在 处的切线方程为
处的切线方程为 ,求证:当
,求证:当 时,曲线
时,曲线 不可能在直线
不可能在直线 的下方;
的下方;
(Ⅲ)若 ,(
,( )且
)且 ,试比较
,试比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
22已知函数![]() ,若方程
,若方程![]() 有且只有两个相异根0和2,且
有且只有两个相异根0和2,且![]() (1)求函数
(1)求函数![]() 的解析式。(2)已知各项不为1的数列{an}满足
的解析式。(2)已知各项不为1的数列{an}满足![]() ,求数列通项an。(3)如果数列{bn}满足
,求数列通项an。(3)如果数列{bn}满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立。
成立。
数学(文)
第I卷(共60分)
一、选择题(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
B
A
A
D
A
C
B
A
A
第Ⅱ卷(共90分)
二、填空题(每小题4分,共16分)
13..files/image277.gif) 14.3 15.97 16.③
14.3 15.97 16.③
三、解答题(共74分)
17.(本小题满分12分)
(I).files/image201.gif) 的内角和
的内角和.files/image280.gif) 。
。
.files/image282.gif) ,
,
.files/image284.gif)
(Ⅱ).files/image286.gif)
.files/image288.gif)
当.files/image290.gif) 即
即.files/image292.gif) 时,
时,.files/image082.gif) 取最大值
取最大值.files/image295.gif)
18.(本题满分12分)
记A:该夫妇生一个小孩是患病男孩,B:该夫妇生一个小孩是患病女孩:C:该夫妇生一个小孩是不患病男孩;D:该夫妇生一个小孩是不患病女孩,则
.files/image297.gif)
(I).files/image299.gif)
.files/image301.gif)
.files/image303.gif)
(Ⅱ)该夫妇所生的前两个是患病男孩,后一个患病女孩的概率为.files/image305.gif) ,所以
,所以
.files/image307.gif)
19.(本题满分12分)
解法一:(I)证明:连接.files/image309.gif) ,设
,设.files/image311.gif) ,连接DE
,连接DE
.files/image313.jpg)
.files/image315.gif) 三棱柱
三棱柱.files/image225.gif) 是正三棱柱,且
是正三棱柱,且.files/image231.gif) ,
,
.files/image319.gif) 四边形
四边形.files/image321.gif) 是正方形,
是正方形,
∴E是.files/image309.gif) 的中点,又
的中点,又.files/image227.gif) 是
是.files/image229.gif) 的中点,
的中点,
∴.files/image326.gif)
∵.files/image328.gif) 平面
平面.files/image330.gif) 平面
平面.files/image235.gif) ,
,
∴.files/image233.gif) 平面
平面.files/image235.gif)
(Ⅱ)解:在平面.files/image335.gif) 内作
内作.files/image337.gif) 于点
于点.files/image339.gif) ,在面
,在面.files/image341.gif) ;内作
;内作.files/image343.gif) 于
于.files/image345.gif) 连接
连接.files/image347.gif) 。
。
∵平面.files/image349.gif) 平面
平面.files/image335.gif) ,∴
,∴.files/image352.gif) 平面
平面.files/image321.gif) ,
,
∵.files/image355.gif) 是
是.files/image347.gif) 在平面
在平面.files/image321.gif) 上的射影,
上的射影,.files/image359.gif)
∴.files/image361.gif) 是二面角
是二面角.files/image237.gif) 的平面角
的平面角
设.files/image364.gif) 在正
在正.files/image201.gif) 中,
中,.files/image367.gif)
在.files/image369.gif) 中,
中,.files/image371.gif) 在
在.files/image373.gif) 中,
中,.files/image375.gif)
从而.files/image377.gif)
所以,二面角.files/image237.gif) 的平面角的余弦值为
的平面角的余弦值为.files/image380.gif)
解法二:建立空间直角坐标系.files/image382.gif) ,如图,
,如图,
(I)证明:连接.files/image384.gif) 设
设.files/image386.gif) ,连接
,连接.files/image388.gif) ,设
,设.files/image390.gif)
.files/image392.jpg) 则
则.files/image394.gif)
.files/image396.gif)
.files/image398.gif)
.files/image400.gif) 平面
平面.files/image330.gif) 平面
平面.files/image403.gif) 平面
平面.files/image235.gif)
(Ⅱ)解:∵.files/image406.gif)
设.files/image408.gif) 是平面
是平面.files/image235.gif) 的法向量,则
的法向量,则.files/image411.gif) ,且
,且.files/image413.gif)
故.files/image415.gif) ,取
,取.files/image417.gif) ,得
,得.files/image419.gif) ;
;
同理,可求得平面.files/image421.gif) 的法向量是
的法向量是.files/image423.gif)
设二面角.files/image237.gif) 的大小为
的大小为.files/image426.gif) ,则
,则.files/image428.gif)
所以,二面角.files/image237.gif) 的平面角的余弦值为
的平面角的余弦值为.files/image380.gif)
20.(本题满分12分)
(I).files/image432.gif) ,依题意,
,依题意,.files/image434.gif) ,即
,即
.files/image436.gif)
解得.files/image438.gif)
.files/image440.gif)
令.files/image442.gif) ,得
,得.files/image444.gif) 或
或.files/image446.gif) 列表可得:
列表可得:
.files/image079.gif)
.files/image449.gif)
.files/image451.gif)
.files/image453.gif)
1
.files/image455.gif)
.files/image457.gif)
+
0
―
0
+
.files/image247.gif)
递增
极大
递减
极小
递增
所以,.files/image460.gif) 是极大值;
是极大值;.files/image462.gif) 是极小值
是极小值
(Ⅱ)曲线方程为.files/image464.gif) 点
点.files/image249.gif) 不在曲线上,
不在曲线上,
设切点为.files/image467.gif) ,则点
,则点.files/image156.gif) 的坐标满足
的坐标满足.files/image470.gif)
因.files/image472.gif) ,故切线的方程为
,故切线的方程为.files/image474.gif)
注意到点.files/image249.gif) 在切线上,有
在切线上,有.files/image477.gif)
化简得.files/image479.gif) ,解得
,解得.files/image481.gif)
21.(本题满分12分)
(I)将.files/image252.gif) 代入
代入.files/image484.gif) 得
得.files/image486.gif) ,整理得
,整理得
.files/image488.gif)
由.files/image490.gif) 得
得.files/image492.gif) ,故
,故
.files/image494.gif)
(Ⅱ)当两条切线的斜率都存在而且不等于.files/image496.gif) 时,设其中一条的斜率为k,
时,设其中一条的斜率为k,
则另外一条的斜率为.files/image498.gif)
于是由上述结论可知椭圆斜率为k的切线方程为
.files/image500.gif) ①
①
又椭圆斜率为.files/image498.gif) 的切线方程为
的切线方程为
.files/image503.gif) ②
②
由①得.files/image505.gif)
由②得.files/image507.gif)
两式相加得.files/image509.gif)
于是,所求P点坐标.files/image511.gif) 满足
满足.files/image513.gif) 因此,
因此,.files/image515.gif)
当一条切线的斜率不存在时,另一条切线的斜率必为0,此时显然也有.files/image517.gif)
所以.files/image519.gif) 为定值。
为定值。
22.(本题满分14分)
(I)由.files/image521.gif) 知
知.files/image523.gif)
当.files/image525.gif) 时,
时,.files/image527.gif) ,化简得
,化简得
.files/image529.gif) ①
①
以.files/image531.gif) 代替
代替.files/image015.gif) 得
得
.files/image534.gif) ②
②
两式相减得
.files/image536.gif)
则.files/image538.gif) ,其中
,其中.files/image525.gif)
所以,数列.files/image120.gif) 为等差数列
为等差数列
(Ⅱ)由.files/image542.gif) ,结合(I)的结论知
,结合(I)的结论知.files/image544.gif)
于是,.files/image546.gif)
.files/image548.gif)
所以,原不等式成立
其他解法参照以上评分标准评分
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com