
题目列表(包括答案和解析)
| n(n+1) | 2 |
| OC |
| OM |
| ON |
| OA |
| OB |
 平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=| 1 | 2 |
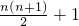 个区域.
个区域.| 1 |
| 2 |
1.B 2.D 3.A 4.C 5.C 6.D 7.D 8.B 9.C 10.B
11.A 12.C
1.理科数学.files/image274.gif) ,所以选B.
,所以选B.
2.理科数学.files/image276.gif) ,所以选D.
,所以选D.
3.理科数学.files/image278.gif) ,所以选
,所以选理科数学.files/image139.gif) .
.
4.理科数学.files/image281.gif) 或
或理科数学.files/image283.gif) ,所以选C.
,所以选C.
5.理科数学.files/image285.gif) ,所以选C.
,所以选C.
6.理科数学.files/image287.gif) ,切线斜率
,切线斜率理科数学.files/image289.gif)
理科数学.files/image291.gif) ,所以选D.
,所以选D.
7.观察图象理科数学.files/image293.gif) .所以选D.
.所以选D.
8.化为理科数学.files/image295.gif) 或
或理科数学.files/image297.gif) ,所以选B.
,所以选B.
9.理科数学.files/image299.gif) 与
与理科数学.files/image301.gif) 关于
关于理科数学.files/image303.gif) 对称,
对称,理科数学.files/image305.gif) ,所以选C.
,所以选C.
10.直线理科数学.files/image110.gif) 与椭圆
与椭圆理科数学.files/image308.gif) 有公共点
有公共点理科数学.files/image310.gif) ,所以选B.
,所以选B.
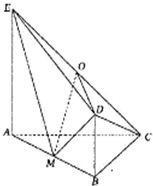
11.如图,设理科数学.files/image312.gif) ,则
,则理科数学.files/image314.gif) ,
,
理科数学.files/image316.jpg)
理科数学.files/image318.gif) ,
,
理科数学.files/image320.gif) ,从而
,从而理科数学.files/image322.gif) ,因此
,因此理科数学.files/image128.gif) 与底面所成角的正弦值等于
与底面所成角的正弦值等于理科数学.files/image325.gif) .所以选A.
.所以选A.
12.分类涂色① 只用3种颜色,相对面同色,有1种涂法;②
用4种颜色,有理科数学.files/image327.gif) 种涂法;③ 用五种颜色,有
种涂法;③ 用五种颜色,有理科数学.files/image329.gif) 种涂法.共有13种涂法.所以选C.
种涂法.共有13种涂法.所以选C.
二、
13.7.由理科数学.files/image331.gif) 或
或理科数学.files/image333.gif) (舍去),
(舍去),
理科数学.files/image335.gif) 项的余数为
项的余数为理科数学.files/image337.gif) .
.
14.依题设理科数学.files/image339.gif) ,又
,又理科数学.files/image145.gif) ,点
,点理科数学.files/image154.gif) 所形成的平面区域为边长为1的正方形,其面积为1.
所形成的平面区域为边长为1的正方形,其面积为1.
15.理科数学.files/image343.gif) ,由
,由理科数学.files/image165.gif) ,得
,得理科数学.files/image346.gif)
理科数学.files/image348.gif) .
.
16.理科数学.files/image350.gif) .
.
理科数学.files/image352.jpg)
如图,可设理科数学.files/image354.gif) ,又
,又理科数学.files/image356.gif) ,
,
理科数学.files/image358.gif) .
.
当理科数学.files/image171.gif) 面积最大时,
面积最大时,理科数学.files/image361.gif) .点
.点理科数学.files/image139.gif) 到直线
到直线理科数学.files/image177.gif) 的距离为
的距离为理科数学.files/image365.gif) .
.
三、
17.(1)理科数学.files/image367.gif)
理科数学.files/image369.gif)
由理科数学.files/image371.gif)
理科数学.files/image373.gif) 得
得理科数学.files/image375.gif) ,
,
理科数学.files/image377.gif) 的单调递减区间为
的单调递减区间为理科数学.files/image379.gif) .
.
(2)理科数学.files/image381.gif)
理科数学.files/image383.gif)
理科数学.files/image385.gif)
理科数学.files/image387.gif)
理科数学.files/image389.gif) .
.
18.(1)理科数学.files/image198.gif) 的所有取值为0.8,0.9,1.0,1.125,1.25,其分布列为
的所有取值为0.8,0.9,1.0,1.125,1.25,其分布列为
理科数学.files/image198.gif)
0.8
0.9
1.0
1.125
1.25
理科数学.files/image393.gif)
0.2
0.15
0.35
0.15
0.15
理科数学.files/image204.gif) 的所有取值为0.8,0.96,1.0,1,2,1.44,其分布列为
的所有取值为0.8,0.96,1.0,1,2,1.44,其分布列为
理科数学.files/image204.gif)
0.8
0.96
1.0
1.2
1.44
理科数学.files/image393.gif)
0.3
0.2
0.18
0.24
0.08
(2)设实施方案一、方案二两年后超过危机前出口额的概率为理科数学.files/image396.gif) ,
,理科数学.files/image398.gif) ,则
,则
理科数学.files/image400.gif)
∴实施方案二两年后超过危机前出口额的概率更大.
(3)方案一、方案二的预计利润为理科数学.files/image402.gif) 、
、理科数学.files/image404.gif) ,则
,则
理科数学.files/image402.gif)
10
15
20
理科数学.files/image393.gif)
0.35
0.35
0.3
理科数学.files/image404.gif)
10
15
20
理科数学.files/image393.gif)
0. 5
0.18
0.32
理科数学.files/image406.gif)
理科数学.files/image408.gif)
∴实施方案一的平均利润更大
19.(1)设理科数学.files/image410.gif) 与
与理科数学.files/image412.gif) 交于点
交于点理科数学.files/image244.gif) .
.
理科数学.files/image415.jpg)
理科数学.files/image417.gif)
理科数学.files/image419.gif)
从而理科数学.files/image421.gif) ,即
,即理科数学.files/image423.gif) ,又
,又理科数学.files/image425.gif) ,且
,且理科数学.files/image427.gif)
理科数学.files/image429.gif) 平面
平面理科数学.files/image431.gif) 为正三角形,
为正三角形,理科数学.files/image433.gif) 为
为理科数学.files/image169.gif) 的中点,
的中点,
理科数学.files/image436.gif) ,且
,且理科数学.files/image438.gif) ,因此,
,因此,理科数学.files/image216.gif) 平面
平面理科数学.files/image126.gif) .
.
(2)理科数学.files/image442.gif) 平面
平面理科数学.files/image126.gif) ,∴平面
,∴平面理科数学.files/image445.gif) 平面
平面理科数学.files/image126.gif) 又
又理科数学.files/image448.gif) ,∴平面
,∴平面理科数学.files/image445.gif) 平面
平面理科数学.files/image451.gif)
设理科数学.files/image163.gif) 为
为理科数学.files/image454.gif) 的中点,连接
的中点,连接理科数学.files/image456.gif) ,则
,则理科数学.files/image458.gif) ,
,
理科数学.files/image460.gif) 平面
平面理科数学.files/image451.gif) ,过点
,过点理科数学.files/image163.gif) 作
作理科数学.files/image464.gif) ,连接
,连接理科数学.files/image466.gif) ,则
,则理科数学.files/image468.gif) .
.
理科数学.files/image470.gif) 为二面角
为二面角理科数学.files/image219.gif) 的平面角.
的平面角.
在理科数学.files/image473.gif) 中,
中,理科数学.files/image475.gif) .
.
又理科数学.files/image477.gif) .
.
20.(1)由理科数学.files/image479.gif) ,得
,得理科数学.files/image481.gif) ,则
,则理科数学.files/image483.gif)
又理科数学.files/image010.gif) 为正整数,
为正整数,理科数学.files/image486.gif)
理科数学.files/image488.gif)
理科数学.files/image490.gif) ,故
,故理科数学.files/image492.gif) .
.
(2)理科数学.files/image494.gif)
理科数学.files/image496.gif)
∴当理科数学.files/image498.gif) 或
或理科数学.files/image500.gif) 时,
时,理科数学.files/image502.gif) 取得最小值
取得最小值理科数学.files/image504.gif) .
.
21.(1)由理科数学.files/image506.gif) 得
得理科数学.files/image508.gif)
∴椭圆理科数学.files/image190.gif) 的方程为:
的方程为:理科数学.files/image511.gif) .
.
(2)由理科数学.files/image258.gif) 得
得理科数学.files/image514.gif) ,
,
理科数学.files/image516.gif)
又理科数学.files/image518.gif)
设直线理科数学.files/image250.gif) 的方程为:
的方程为:理科数学.files/image521.gif)
由理科数学.files/image523.gif) 得
得理科数学.files/image525.gif)
理科数学.files/image527.gif)
理科数学.files/image529.gif)
由此得理科数学.files/image531.gif) . ①
. ①
设理科数学.files/image250.gif) 与椭圆
与椭圆理科数学.files/image190.gif) 的交点为
的交点为理科数学.files/image535.gif) ,则
,则理科数学.files/image537.gif)
由理科数学.files/image539.gif) 得
得理科数学.files/image541.gif)
理科数学.files/image543.gif) ,整理得
,整理得理科数学.files/image545.gif)
理科数学.files/image547.gif) ,整理得
,整理得理科数学.files/image549.gif)
理科数学.files/image551.gif) 时,上式不成立,
时,上式不成立,理科数学.files/image553.gif) ②
②
由式①、②得理科数学.files/image555.gif)
理科数学.files/image557.gif) 或
或理科数学.files/image559.gif)
∴理科数学.files/image262.gif) 取值范围是
取值范围是理科数学.files/image562.gif) .
.
22.(1)由理科数学.files/image564.gif) 得
得理科数学.files/image566.gif)
令理科数学.files/image568.gif) ,则
,则理科数学.files/image570.gif)
当理科数学.files/image572.gif) 时,
时,理科数学.files/image574.gif) 在
在理科数学.files/image576.gif) 上单调递增.
上单调递增.
理科数学.files/image578.gif)
理科数学.files/image580.gif) 的取值范围是
的取值范围是理科数学.files/image582.gif) .
.
(2)理科数学.files/image584.gif)
则理科数学.files/image586.gif)
① 当理科数学.files/image588.gif) 时,
时,理科数学.files/image590.gif) 是减函数.
是减函数.
理科数学.files/image592.gif) 时,
时,理科数学.files/image594.gif) 是增函数.
是增函数.
② 当理科数学.files/image596.gif) 时,
时,理科数学.files/image598.gif) 是增函数.
是增函数.
综上;当理科数学.files/image588.gif) 时,增区间为
时,增区间为理科数学.files/image601.gif) ,,减区间为
,,减区间为理科数学.files/image603.gif) ;
;
当理科数学.files/image596.gif) 时,增区间为
时,增区间为理科数学.files/image606.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com