
题目列表(包括答案和解析)
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
【解析】第一问当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
第二问当 时,
时, ,令
,令 得
得 ,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
第三问假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
(Ⅰ)当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①当 时,
时, ,令
,令 得
得
当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
极小值 |
单调递增 |
极大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值为2.
上的最大值为2.
②当 时,
时,  .当
.当 时,
时,  ,
, 最大值为0;
最大值为0;
当 时,
时,  在
在 上单调递增。∴
上单调递增。∴ 在
在 最大值为
最大值为 。
。
综上,当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为2;
上的最大值为2;
当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为
上的最大值为 。
。
(Ⅲ)假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
若 ,则
,则 代入(*)式得:
代入(*)式得:
即 ,而此方程无解,因此
,而此方程无解,因此 。此时
。此时 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,则
,则
∴ 在
在 上单调递增, ∵
上单调递增, ∵  ∴
∴ ,∴
,∴ 的取值范围是
的取值范围是 。
。
∴对于 ,方程(**)总有解,即方程(*)总有解。
,方程(**)总有解,即方程(*)总有解。
因此,对任意给定的正实数 ,曲线
,曲线 上存在两点P、Q,使得
上存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上
轴上
设定义在R的函数![]() ,
,![]() R. 当
R. 当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,且函数
,且函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
(I)求函数![]() 的表达式;
的表达式;
(II)判断函数![]() 的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间
的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间![]() 上,并说明理由;
上,并说明理由;
![]() (III)设
(III)设![]() ,
,![]() (
(![]() ),求证:
),求证:![]() .
.
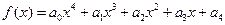 ,
,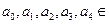 R. 当
R. 当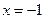 时,
时,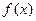 取得极大值
取得极大值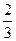 ,且函数
,且函数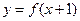 的图象关于点
的图象关于点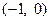 对称.
对称.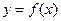 的表达式;
的表达式;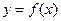 的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间
的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间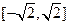 上,并说明理由;
上,并说明理由; (III)设
(III)设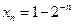 ,
,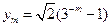 (
(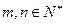 ),求证:
),求证: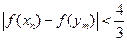 .
. 时,f(x)取得极大值
时,f(x)取得极大值 ,并且函数y=f'(x)的图象关于y轴对称.
,并且函数y=f'(x)的图象关于y轴对称.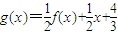 ,求曲线C过点P(2,4)的切线方程;
,求曲线C过点P(2,4)的切线方程; 可作曲线y=f(x)的三条切线,求实数m的取值范围.
可作曲线y=f(x)的三条切线,求实数m的取值范围. 时,f(x)取得极大值
时,f(x)取得极大值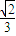 ,并且函数y=f′(x)的图象关于y轴对称.
,并且函数y=f′(x)的图象关于y轴对称. ,求曲线过点P(2,4)的切线方程.
,求曲线过点P(2,4)的切线方程.一、选择题(本大题共有8个小题,每小题5分,共40分;在每个小题给出的四个选项中有且仅有一个符合题目要求的)
题号
1
2
3
4
5
6
7
8
答案
B
D
C
C
B
A
C
B
二、填空题(本大题共有6个小题,每小题5分,共30分;请把答案填在相应的位置)
题号
9
10
11
12
13
14
答案
-1+.files/image239.gif)
8,70
24
.files/image241.gif)
.files/image243.gif)
①③④
三、解答题(本大题共6个小题,共80分;解答应写出文字说明,证明过程或演算步骤)
15.(本题满分13分)
解:(1).files/image245.gif)
.files/image247.gif)
.files/image249.gif)
(2)由题意,得
.files/image251.gif)
16.(本题满分13分)
解:(1)这3封信分别被投进3个信箱的概率为
.files/image253.gif)
(2)恰有2个信箱没有信的概率为
.files/image255.gif)
(3)设信箱.files/image153.gif) 中的信箱数为
中的信箱数为.files/image258.gif)
.files/image260.gif)
.files/image262.gif)
0
1
2
3
.files/image210.gif)
.files/image265.gif)
.files/image265.gif)
.files/image268.gif)
.files/image270.gif)
17.(本题满分13分)
解:解答一:(1)在菱形.files/image272.gif) 中,连接
中,连接.files/image274.gif) 则
则.files/image276.gif) 是等边三角形。
是等边三角形。
.files/image278.gif)
(2).files/image280.gif)
.files/image282.jpg)
.files/image284.gif)
.files/image286.gif)
(3)取.files/image288.gif) 中点
中点.files/image290.gif) ,连结
,连结.files/image292.gif)
.files/image294.gif)
解法二:(1)同解法一;
(2)过点.files/image165.gif) 作
作.files/image288.gif) 平行线交
平行线交.files/image298.gif) 于
于.files/image300.gif) ,以点
,以点.files/image165.gif) 为坐标原点,建立如图的坐标系
为坐标原点,建立如图的坐标系
.files/image303.gif)
.files/image305.gif) 二面角
二面角.files/image307.gif) 的大小为
的大小为.files/image309.gif)
(3)由已知,可得点.files/image311.gif)
.files/image313.gif)
即异面直线.files/image315.gif) 所成角的余弦值为
所成角的余弦值为.files/image317.gif)
18.(本题满分13分)
解:(1)将函数.files/image186.gif) 的图象向右平移一个单位,得到函数
的图象向右平移一个单位,得到函数.files/image074.gif) 的图象,
的图象,
.files/image305.gif) 函数
函数.files/image074.gif) 的图象关于点(0,0)对称,即函数
的图象关于点(0,0)对称,即函数.files/image074.gif) 是奇函数,
是奇函数,
.files/image324.gif)
.files/image326.gif)
由题意得:.files/image328.gif)
所以.files/image330.gif)
(2)由(1)可得.files/image332.gif)
故设所求两点为.files/image334.gif)
.files/image336.gif)
.files/image305.gif) 满足条件的两点的坐标为:
满足条件的两点的坐标为:.files/image339.gif)
(3).files/image341.gif)
.files/image343.gif)
.files/image345.gif)
19.(本题满分14分)
解:(1)椭圆.files/image200.gif) 的右焦点
的右焦点.files/image204.gif) 的坐标为(1,0),
的坐标为(1,0),
.files/image349.gif)
(2).files/image351.gif)
.files/image353.gif)
(3)由(2)知.files/image355.gif)
.files/image357.gif)
20.(本题满分14分)
解:(1).files/image359.gif)
.files/image361.gif)
(2)由(1)知.files/image363.gif)
.files/image365.gif)
(3).files/image367.gif)
.files/image369.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com