
题目列表(包括答案和解析)
意大利数学家斐波那契在他的1228年版的《算经》一书中记述了有趣的兔子问题:假定每对大兔子每月能生一对小兔子,而每对小兔子过了一个月就可长成大兔子,如果不发生死亡,那么由一对大兔子开始,一年后能有多少对大兔子呢?
我们依次给出各个月的大兔子对数,并一直推算下去到无尽的月数,可得数列:1,1,2,3,5,8,13,21,34,55,89,144,233,….这就是斐波那契数列,此数列中a1=a2=1,你能归纳出,当n≥3时,an的递推关系吗?
意大利数学家斐波那契(L.Fibonacci)在他的1228年版的《算经》一书中记述了有趣的兔子问题:假定每对大兔子每月能生一对小兔子,而每对小兔子过了一个月就可长成大兔子,如果不发生死亡,那么由一对大兔子开始,一年后能有多少对大兔子呢?
我们依次给出各个月的大兔子对数,并一直推算下去到无尽的月数,可得数列:
1,1,2,3,5,8,13,21,34,55,89,144,233,……
这就是斐波那契数列,此数列中a1=a2=1,你能归纳出当n≥3时an的递推关系式吗?
意大利数学家斐波那契(L.Fibonacci)在他的1228年版的《算经》一书中记述了有趣的兔子问题:假定每对大兔子每月能生一对小兔子,而每对小兔子过了一个月就可长成大兔子.如果不发生死亡,那么由一对大兔子开始,一年后能有多少对大兔子呢?
我们依次给出各个月的大兔子对数,并一直推算下去到无尽的月数,可得数列:
1,1,2,3,5,8,13,21,34,55,89,144,233,….
这就是斐波那契数列,此数列中a1=a2=1,你能归纳出,当n≥3时an的递推关系式吗?
| 2 | ||
|
| MA |
| MB |
| AB |
(本题满分13分)
对于给定数列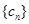 ,如果存在实常数
,如果存在实常数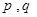 使得
使得 对于任意
对于任意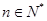 都成立,我们称数列
都成立,我们称数列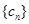 是 “M类数列”.
是 “M类数列”.
(1)若 ,
, ,
,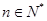 ,数列
,数列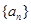 、
、 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列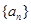 是“M类数列”,则数列
是“M类数列”,则数列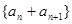 也是“M类数列”;
也是“M类数列”;
(3)若数列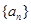 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列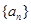 前
前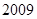 项的和.
项的和.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com