如图1，已知矩形OABC中，OC=10，OA=6，在OA、OC边上选取适当的点E、F，将△OEF沿EF对折，使O点落在AB边上的D点．
（1）当点E取在点A上，得图2，求出相应的OF的长；
（2）写出OF的取值范围；
（3）在如图1中过点D作DG∥AO交EF于点T，交OC于点G，连接OT，得到图3
①证明四边形OEDT是菱形；
②设AD长为x，请你利用所学的函数及其图象的有关知识判断，当x取什么值时，菱形OEDT的周长L取最大值，并求出周长L的最大值．

如图1，已知矩形OABC中，OC=10，OA=6，在OA、OC边上选取适当的点E、F，将△OEF沿EF对折，使O点落在AB边上的D点．
（1）当点E取在点A上，得图2，求出相应的OF的长；
（2）写出OF的取值范围；
（3）在如图1中过点D作DG∥AO交EF于点T，交OC于点G，连接OT，得到图3
①证明四边形OEDT是菱形；
②设AD长为x，请你利用所学的函数及其图象的有关知识判断，当x取什么值时，菱形OEDT的周长L取最大值，并求出周长L的最大值．

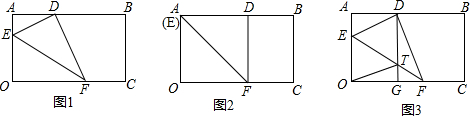
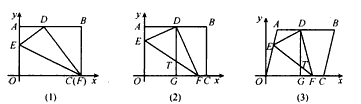
将边长OA=8，OC=10的矩形OABC放在平面直角坐标系中，顶点O为原点，顶点C、A分别在x轴和y轴上．在OA、OC边上选取适当的点E、F，连接EF，将△EOF沿EF折叠，使点O落在AB边上的点D处．

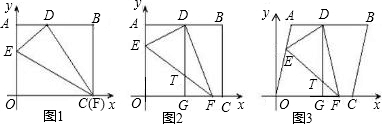
（1）如图1，当点F与点C重合时，OE的长度为；
（2）如图2，当点F与点C不重合时，过点D作DG∥y轴交EF于点T，交OC于点G．求证：EO=DT；
（3）在（2）的条件下，设T（x，y），写出y与x之间的函数关系式为，自变量x的取值范围是；
（4）如图3，将矩形OABC变为平行四边形，放在平面直角坐标系中，且OC=10，OC边上的高等于8，点F与点C不重合，过点D作DG∥y轴交EF于点T，交OC于点G，求出这时T（x，y）的坐标y与x之间的函数关系式（不求自变量x的取值范围）．