
题目列表(包括答案和解析)
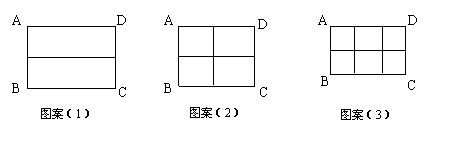
初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,根据以下图案,小组发现在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6米,当AB为1米,时长方形框架ABCD的面积是1×![]() =
=![]() m2;在图案(2)中,如果铝合金材料总长度为6米,设AB为1米,长方形框架ABCD的面积是1×1=
m2;在图案(2)中,如果铝合金材料总长度为6米,设AB为1米,长方形框架ABCD的面积是1×1=![]() =1m2,请你回答:在图案(3)中,如果铝合金材料总长度为6米, 设AB为
=1m2,请你回答:在图案(3)中,如果铝合金材料总长度为6米, 设AB为![]() 米, 长方形框架ABCD的面积为S,
米, 长方形框架ABCD的面积为S,
(1)求S与x的函数关系式;
(2)当AB是多少米时, 长方形框架ABCD的面积为![]() .
.
 |
初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:
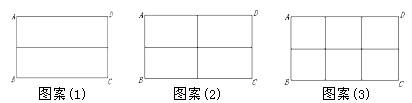
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,
长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为![]() m,长方形框架ABCD的面积为S= (用含
m,长方形框架ABCD的面积为S= (用含![]() 的代数式表示);当AB= m时, 长方形框架ABCD的面积S最大;
的代数式表示);当AB= m时, 长方形框架ABCD的面积S最大;
(3)在图案(3)中,如果铝合金材料总长度为![]() m, 设AB为
m, 设AB为![]() m,求出ABCD的面积S与
m,求出ABCD的面积S与![]() 的函数关系式,并求出当AB为多少m时, 长方形框架ABCD的面积S最大.
的函数关系式,并求出当AB为多少m时, 长方形框架ABCD的面积S最大.
初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们做了以下三种试验:
请根据以下图案回答问题:(1)在图①中,如果铝合金材料总长度(图中所有黑线的长度和)为6 m,当AB为1 m时,长方形框架ABCD的面积是_________
(2)
在图②中,如果铝合金材料总长度为6 m,设AB为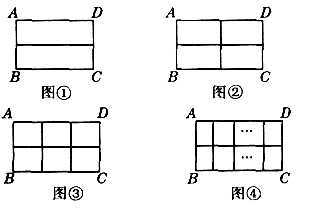
(3)
经过这三种情形的试验,他们发现对于图④这样的情形也存在着一定的规律.那么这个规律是什么?请加以证明
初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
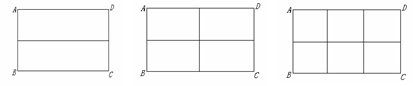 |
图案(1) 图案(2) 图案(3)
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6米,当AB为1米,
长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6米,设AB为![]() 米,长方形框架ABCD的面积为S= (用含
米,长方形框架ABCD的面积为S= (用含![]() 的代数式表示);当AB= 时米, 长方形框架ABCD的面积S最大;
的代数式表示);当AB= 时米, 长方形框架ABCD的面积S最大;
在图案(3)中,如果铝合金材料总长度为米, 设AB为![]() 米,当AB是多少米时, 长方形框架ABCD的面积S最大.
米,当AB是多少米时, 长方形框架ABCD的面积S最大.
初三(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
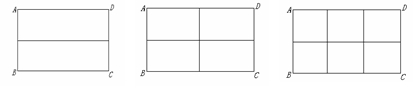 |
图案(1) 图案(2) 图案(3)
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6米,当AB为1米,
长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6米,设AB为![]() 米,长方形框架ABCD的面积为S= (用含
米,长方形框架ABCD的面积为S= (用含![]() 的代数式表示);当AB= 时米, 长方形框架ABCD的面积S最大;
的代数式表示);当AB= 时米, 长方形框架ABCD的面积S最大;
在图案(3)中,如果铝合金材料总长度为米, 设AB为![]() 米,当AB是多少米时, 长方形框架ABCD的面积S最大.
米,当AB是多少米时, 长方形框架ABCD的面积S最大.
说明:对于解题过程中有的题目可用多种解法(或多种证明方法),如果考生的解答与参考答案不同,请参照此评分标准酌情给分.
一. 选择题(本题共10小题,每小题4分,共40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
B
D
B
A
D
C
C
评分标准
选对一题给4分,不选,多选,错选均不给分
二、填空题(本题有6小题,每小题5分,共30分)
11.X≠6 ; 12. 2 ; 13.8;
14. 65°;
; 13.8;
14. 65°;
15.96 ; 16. (0,0),(0, ),(0,-3)写对一个给3分,两个4分,三个给5分
),(0,-3)写对一个给3分,两个4分,三个给5分
三、解答题(本题有8小题,共80分)
17. (本题8分)
(1)解:原式=1+3- …………(3分)
…………(3分)
= …………(1分)
…………(1分)
(2)解:愿方程可化为:x=3(x-2 ) …………(2分)
x=3 …………(1分)
经检验 :x=3 是原方程的解. …………(1分)
18.(本题8分)
添加条件例举:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等. ……(2分)
证明例举(以添加条件AD=BC为例):
∵ AB=AB,∠1=∠2,BC=AD, …………(2分)
∴ △ABC≌△BAD. …………(2分)
∴ AC=BD. …………(2分)
19.(本题8分)
(1) ; …………(3分)
; …………(3分)
(2)列对表格或画对树状图; …………(3分)
两次都取到欢欢的概率为 . …………(2分)
. …………(2分)
20.(本题8分)
答案不唯一.只要符合要求,画对一个给4分,画对两个给8分. ……(8分)
21.(本题8分)
(1)∵AB是⊙O直径,∴∠ACB=Rt∠.∴sin∠BAC= . ………(3分)
. ………(3分)
(2)∵OE⊥AC,O是⊙O的圆心, ∴E是AC中点.∴OE= BC=
BC= . …(3分)
. …(3分)
(3)∵AC= =4, ∴tan∠ADC= tan∠ABC=
=4, ∴tan∠ADC= tan∠ABC= .
……(2分)
.
……(2分)
22.(本题10分)
(1) 25 ; ……………(2分)
(2) 50; ……………(2分)
画对条形统计图 ……………(2分)
(3)5人;(列对方程得2分,给出答案给2分) ……………(4分)
23.(本题12分)
(1) ;
………………(2分)
;
………………(2分)
(2)-x2+2x ,1, ; (每格2分)
……………(6分)
; (每格2分)
……………(6分)
(3)设AB长为 m,那么AD为
m,那么AD为
S= ?
? =-
=- . ……………(2分)
. ……………(2分)
当 =
= 时,S最大. ……………(2分)
时,S最大. ……………(2分)
24.(本题14分)
(1)直线AB解析式为:y= x+
x+ .
……………(3分)
.
……………(3分)
(2)方法一:设点C坐标为(x, x+
x+ ),那么OD=x,CD=
),那么OD=x,CD= x+
x+ .
.
∴ =
= =
= .
………(2分)
.
………(2分)
由题意: =
= ,解得
,解得 (舍去) ………(2分)
(舍去) ………(2分)
∴ C(2, ) ………(1分)
) ………(1分)
方法二:∵  ,
, =
= ,∴
,∴ .…(2分)
.…(2分)
由OA= OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD= CD.
CD.
∴  =
= CD×AD=
CD×AD= =
= .可得CD=
.可得CD= . ………(2分)
. ………(2分)
 ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2, ). ………(1分)
). ………(1分)
(3)当∠OBP=Rt∠时,如图
①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP= OB=3,
OB=3,
∴ (3,
(3, ).
……(2分)
).
……(2分)
②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP= OB=1.
OB=1.
∴ (1,
(1, ). …………(1分)
). …………(1分)
当∠OPB=Rt∠时
③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30°
 过点P作PM⊥OA于点M.
过点P作PM⊥OA于点M.
方法一: 在Rt△PBO中,BP= OB=
OB= ,OP=
,OP= BP=
BP= .
.
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM= OP=
OP= ;PM=
;PM= OM=
OM= .∴
.∴ (
( ,
, ). ……(1分)
). ……(1分)
 方法二:设P(x ,
方法二:设P(x , x+
x+ ),得OM=x ,PM=
),得OM=x ,PM= x+
x+
由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM== =
= ,tan∠ABOC=
,tan∠ABOC= =
= .
.
∴ x+
x+ =
= x,解得x=
x,解得x= .此时,
.此时, (
( ,
, ). ……(1分)
). ……(1分)
④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°.
∴ PM= OM=
OM= .
.
∴  (
( ,
, )(由对称性也可得到点
)(由对称性也可得到点 的坐标).…………(2分)
的坐标).…………(2分)
当∠OPB=Rt∠时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:
 (3,
(3, ),
), (1,
(1, ),
), (
( ,
, ),
), (
( ,
, ).
).
注:四个点中,求得一个P点坐标给2分,两个给3分,三个给4分,四个给6分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com