练习册

  • 练习册
  • 试题
    【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分13分）有一问题，在半小时内，甲能解决它的概率是0.5，乙能解决它的概率是，

     如果两人都试图独立地在半小时内解决它，计算：w.w.w.k.s.5.u.c.o.m      

       （1）两人都未解决的概率；

       （2）问题得到解决的概率。

    查看答案和解析>>

    （本小题满分13分）  已知是等比数列, ；是等差数列, , .

    (1) 求数列、的通项公式；

    (2) 设+…+,…,其中,…试比较与的大小,并证明你的结论.

    查看答案和解析>>

    （本小题满分13分） 现有一批货物由海上从A地运往B地，已知货船的最大航行速度为35海里/小时，A地至B地之间的航行距离约为500海里，每小时的运输成本由燃料费和其余费用组成，轮船每小时的燃料费用与轮船速度的平方成正比（比例系数为0.6），其余费用为每小时960元.

    （1）把全程运输成本y(元)表示为速度x(海里/小时)的函数；

    （2）为了使全程运输成本最小，轮船应以多大速度行驶？

    查看答案和解析>>

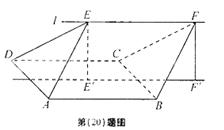
    （本小题满分13分）

    如图，ABCD的边长为2的正方形，直线l与平面ABCD平行，g和F式l上的两个不同点，且EA=ED，FB=FC， 和是平面ABCD内的两点，和都与平面ABCD垂直，

    （Ⅰ）证明：直线垂直且平分线段AD：w.w.w.k.s.5.u.c.o.m       

    （Ⅱ）若∠EAD=∠EAB=60°，EF=2，求多面

    体ABCDEF的体积。

     

    查看答案和解析>>

    （本小题满分13分）两个人射击，甲射击一次中靶概率是p1，乙射击一次中靶概率是p2，已知 , 是方程x2－5x + 6 = 0的根，若两人各射击5次，甲的方差是 ．(1) 求 p1、p2的值；(2) 两人各射击2次，中靶至少3次就算完成目的，则完成目的的概率是多少？(3) 两人各射击一次，中靶至少一次就算完成目的，则完成目的的概率是多少？

    查看答案和解析>>

    一、A；A；C；D；A；A； C；C；B；C；C；A

    二、13、高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。或高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。； 14、80；  15、-2；16、高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ；

    17、解：⑴高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………………………………………3分

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，由高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得函数的递增区间为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，由高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得函数的递增区间为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………………………………………5分

    ⑵高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………7分

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。（舍）

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    综上，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………………10分

    18、解：用高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。分别表示三列火车正点到达的事件，则

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ⑴恰有两列火车正点到达的概率记为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,则

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………4分

    ⑵用高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。表示误点的列数，则至少两列误点可表示为：

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………………………………………………………6分

    19．解：方法一：（I）证明：，

    又高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。平面平面ABCD，平面平面ABCD＝BC，

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    平面ABCD ……2分

       在梯形ABCD中，可得

       ，即

        在平面ABCD内的射影为AO，                  ……4分

       （II）解：，且平面平面ABCD

        平面PBC， 平面PBC，

        为二面角P―DC―B的平面角                                 ……6分

        是等边三角形即二面角P―DC―B的大小为 …8分

     （III）证明：取PB的中点N，连结CN，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ①

        ，且平面平面ABCD，平面PBC  ……10分

        平面PAB    平面平面PAB  ②

         由①、②知平面PAB…………..10分

    连结DM、MN，则由MN//AB//CD，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    得四边形MNCD为平行四边形，，平面PAB．

    平面PAD    平面平面PAB ……………….12分

    方法二：取BC的中点O，因为是等边三角形，

        由侧面底面ABCD    得底面ABCD ……1分

    以BC中点O为原点，以BC所在直线为x轴，过点O与AB平行的直线为y轴，建立如图所示的空间直角坐标系O―xyz……2分

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （I）证明：，则在直角梯形中，

        在等边三角形PBC中，……3分

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，即…4分

     （II）解：取PC中点N，则高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        平面PDC，显然，且平面ABCD

        所夹角等于所求二面角的平面角                         ……6分

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

     高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，二面角的大小为             ……8分

    （III）证明：取PA的中点M，连结DM，则M的坐标为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        又高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                                         ……10分

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即

    平面PAB，平面平面PAB                         ……12分

    20．解：Ⅰ由已知得：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ……………………………………2分

    当高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。解得：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………………………………………3分

    当高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，带入上式得：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    配方得：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    所以高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………5分

    所以高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………7分

    Ⅱ高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………………………………10分

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………………………12分

    21．解：（I）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。右准线高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，渐近线高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                 ……3分

        （II）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。双曲线C的方程为：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。               ……7分

        （III）由题意可得高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                           ……8分

        证明：设高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，点高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        由高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。得高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。与双曲线C右支交于不同的两点P、Q

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                            ……11分

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，得高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

        高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的取值范围是（0，1）                            ……13分

    22解：⑴高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    则高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………3分

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；由此可知

    当高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，函数高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。单调递增

    当高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，函数高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。单调递减，

    当高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，函数取极大值高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………………………6分

    ⑵高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在区间高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上是单调减函数，

    所以高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在区间高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上恒成立，有二次函数的图像可知：

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；令高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………………………………………9分

    当直线高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。经过交点高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，取得最小值高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………………………………13分

     

     

     

     

     


    同步练习册答案