
题目列表(包括答案和解析)
| 2 |
| 3 |
| 1 |
| 3 |
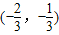 是减函数.
是减函数.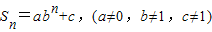 则此数列是等比数列的充要条件是a+c=0.
则此数列是等比数列的充要条件是a+c=0.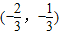 是减函数.
是减函数.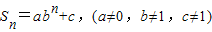 则此数列是等比数列的充要条件是a+c=0.
则此数列是等比数列的充要条件是a+c=0.| a |
| 2 |
| a |
| 2 |
说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.
2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分.
一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.
题号
1
2
3
4
5
6
7
8
答案
B
C
D
A
D
A
C
B
8.方法1:由.files/image106.gif) ,得
,得.files/image283.gif) ,
,
即.files/image285.gif) .
.
于是.files/image287.gif) ,
,
所以.files/image289.gif) .
.
方法2:由.files/image106.gif) ,得
,得.files/image283.gif) ,
,
即.files/image285.gif) .
.
于是.files/image291.gif) ,
,
则.files/image293.gif) (其中
(其中.files/image295.gif) ),再利用导数的方法求解.
),再利用导数的方法求解.
二、填空题:本大题主要考查基本知识和基本运算.共7小题,每小题5分,满分30分.
9.760 10..files/image297.gif) 11.2 12.
11.2 12..files/image299.gif)
13..files/image301.gif) 14.
14..files/image303.gif) 15.3
15.3
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
(本小题主要考查正弦定理、余弦定理、解三角形等基础知识,考查运算求解能力)
解:(1)由余弦定理,.files/image305.gif) ,………………………………………2分
,………………………………………2分
得.files/image307.gif) ,…………………………………………………4分
,…………………………………………………4分
.files/image309.gif)
.files/image311.gif) .……………………………………………………………………………6分
.……………………………………………………………………………6分
(2)方法1:由余弦定理,得.files/image313.gif) ,………………………………8分
,………………………………8分
.files/image315.gif) ,………………………10分
,………………………10分
∵.files/image243.gif) 是
是.files/image318.gif) 的内角,
的内角,
∴.files/image320.gif) .………………………………………………………12分
.………………………………………………………12分
方法2:∵.files/image195.gif) ,且
,且.files/image004.gif) 是
是.files/image318.gif) 的内角,
的内角,
∴.files/image324.gif) .………………………………………………………8分
.………………………………………………………8分
根据正弦定理,.files/image326.gif) ,……………………………………………………10分
,……………………………………………………10分
得.files/image328.gif) . ……………………………………………12分
. ……………………………………………12分
17.(本小题满分12分)
(本小题主要考查独立重复试验等基础知识,考查或然与必然的数学思想与方法,以及运算求解能力)
解:(1)设“甲射击5次,恰有3次击中目标”为事件A,则
.files/image330.gif) .
.
答:甲射击5次,恰有3次击中目标的概率为.files/image332.gif) .………………………………6分
.………………………………6分
(2)方法1:设“甲恰好射击5次后,被中止射击”为事件C,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则
.files/image334.gif) .
.
答:甲恰好射击5次后,被中止射击的概率为.files/image336.gif) .……………………………12分
.……………………………12分
方法2:设“甲恰好射击5次后,被中止射击”为事件C,由于甲恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第三次击中目标,第一次与第二次至少有一次击中目标,则
.files/image338.gif) .
.
答:甲恰好射击5次后,被中止射击的概率为.files/image336.gif) .……………………………12分
.……………………………12分
18.(本小题满分14分)
(本小题主要考查空间中线面关系,二面角及其平面角、坐标方法的运用等基础知识,考查数形结合的数学思想和方法,以及空间想象能力、逻辑推理能力和运算求解能力)
(1)证法1:∵.files/image207.gif) 平面
平面.files/image205.gif) ,
,.files/image342.gif) 平面
平面.files/image205.gif) ,∴
,∴.files/image344.gif) .
.
又.files/image205.gif) 为正方形,∴
为正方形,∴.files/image346.gif) .
.
∵.files/image348.gif) ,∴
,∴.files/image350.gif) 平面
平面.files/image352.gif) .……………………………………………3分
.……………………………………………3分
∵.files/image354.gif) 平面
平面.files/image352.gif) ,∴
,∴.files/image356.gif) .
.
∵.files/image358.gif) ,∴
,∴.files/image220.gif) .…………………………………………………………6分
.…………………………………………………………6分
证法2:以.files/image252.gif) 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系.files/image362.gif) ,
,
则.files/image364.gif) ,
,.files/image366.gif) ,
,.files/image368.gif) ,
,.files/image370.gif) ,
,.files/image372.gif) ,
,.files/image374.gif) .
.
…………………………………………………4分
.files/image375.gif) ∵
∵.files/image377.gif) ,
,
∴.files/image220.gif) .………………………………………6分
.………………………………………6分
(2)解法1:以.files/image252.gif) 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系.files/image362.gif) ,
,
则.files/image379.gif) ,
,.files/image364.gif) ,
,.files/image381.gif) ,
,.files/image366.gif) ,
,
.files/image383.gif) ,
,.files/image374.gif) ,
,.files/image385.gif) .………………………………8分
.………………………………8分
设平面DFG的法向量为.files/image387.gif) ,
,
∵.files/image389.gif)
令.files/image391.gif) ,得
,得.files/image393.gif) 是平面
是平面.files/image395.gif) 的一个法向量.…………………………10分
的一个法向量.…………………………10分
设平面EFG的法向量为.files/image397.gif) ,
,
∵.files/image399.gif)
令.files/image401.gif) ,得
,得.files/image403.gif) 是平面
是平面.files/image405.gif) 的一个法向量.……………………………12分
的一个法向量.……………………………12分
∵.files/image407.gif) .
.
设二面角.files/image409.gif) 的平面角为θ,则
的平面角为θ,则.files/image411.gif) .
.
所以二面角.files/image409.gif) 的余弦值为
的余弦值为.files/image413.gif) .………………………………………14分
.………………………………………14分
解法2:以.files/image252.gif) 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系.files/image362.gif) ,
,
则.files/image379.gif) ,
,.files/image364.gif) ,
,.files/image381.gif) ,
,.files/image366.gif) ,
,.files/image383.gif) ,
,.files/image415.gif) ,
,.files/image374.gif) ,
,.files/image417.gif) ,
,.files/image385.gif) .………………………………8分
.………………………………8分
.files/image419.gif) 过
过.files/image252.gif) 作
作.files/image422.gif) 的垂线,垂足为
的垂线,垂足为.files/image134.gif) ,
,
∵.files/image425.gif) 三点共线,∴
三点共线,∴.files/image427.gif) ,
,
∵.files/image429.gif) ,∴
,∴.files/image431.gif) ,
,
即.files/image433.gif) ,解得
,解得.files/image435.gif) .
.
∴.files/image437.gif) .…………10分
.…………10分
再过.files/image175.gif) 作
作.files/image422.gif) 的垂线,垂足为
的垂线,垂足为.files/image440.gif) ,
,
∵.files/image442.gif) 三点共线,∴
三点共线,∴.files/image444.gif) ,
,
∵.files/image446.gif) ,∴
,∴.files/image448.gif) ,
,
即.files/image450.gif) ,解得
,解得.files/image452.gif) .
.
∴.files/image454.gif) .……………………………………………12分
.……………………………………………12分
∴.files/image456.gif) .
.
∵.files/image458.gif) 与
与.files/image460.gif) 所成的角就是二面角
所成的角就是二面角.files/image409.gif) 的平面角,
的平面角,
所以二面角.files/image409.gif) 的余弦值为
的余弦值为.files/image413.gif) .………………………………………14分
.………………………………………14分
19.(本小题满分14分)
(本小题主要考查函数、微积分基本定理和导数的应用,考查综合运用数学知识分析和解决问题的能力)
解:(1)函数.files/image462.gif) 的定义域为
的定义域为.files/image464.gif) ,…………………………………………………1分
,…………………………………………………1分
∵.files/image466.gif) ,………………………………………2分
,………………………………………2分
∵.files/image468.gif) ,则使
,则使.files/image470.gif) 的
的.files/image225.gif) 的取值范围为
的取值范围为.files/image473.gif) ,
,
故函数.files/image462.gif) 的单调递增区间为
的单调递增区间为.files/image473.gif) . ……………………………………………4分
. ……………………………………………4分
(2)方法1:∵.files/image222.gif) ,
,
∴.files/image476.gif) .…………………………6分
.…………………………6分
令.files/image478.gif) ,
,
∵.files/image480.gif) ,且
,且.files/image468.gif) ,
,
由.files/image483.gif) .
.
∴.files/image485.gif) 在区间
在区间.files/image487.gif) 内单调递减,在区间
内单调递减,在区间.files/image489.gif) 内单调递增,……………………9分
内单调递增,……………………9分
故.files/image491.gif) 在区间
在区间.files/image229.gif) 内恰有两个相异实根
内恰有两个相异实根.files/image494.gif) ……12分
……12分
即.files/image496.gif) 解得:
解得:.files/image498.gif) .
.
综上所述,.files/image231.gif) 的取值范围是
的取值范围是.files/image501.gif) .………………………………14分
.………………………………14分
方法2:∵.files/image222.gif) ,
,
∴.files/image476.gif) .…………………………6分
.…………………………6分
即.files/image503.gif) ,
,
令.files/image505.gif) ,
,
∵.files/image507.gif) ,且
,且.files/image468.gif) ,
,
由.files/image509.gif) .
.
∴.files/image511.gif) 在区间
在区间.files/image487.gif) 内单调递增,在区间
内单调递增,在区间.files/image489.gif) 内单调递减.……………………9分
内单调递减.……………………9分
∵.files/image513.gif) ,
,.files/image515.gif) ,
,.files/image517.gif) ,
,
又.files/image519.gif) ,
,
故.files/image491.gif) 在区间
在区间.files/image229.gif) 内恰有两个相异实根
内恰有两个相异实根.files/image521.gif) .
.
……………………………………12分
即.files/image498.gif) .
.
综上所述,.files/image231.gif) 的取值范围是
的取值范围是.files/image501.gif) . ……………………………14分
. ……………………………14分
20.(本小题满分14分)
(本小题主要考查椭圆的概念、椭圆的方程等基础知识,考查待定系数法、数形结合的数学思想与方法,以及运算求解能力)
解:(1)设点.files/image134.gif) 的坐标为
的坐标为.files/image524.gif) ,
,
∵.files/image526.gif) ,∴
,∴.files/image528.gif) . ………………………………………2分
. ………………………………………2分
整理,得.files/image530.gif) (
(.files/image532.gif) ),这就是动点M的轨迹方程.……………………4分
),这就是动点M的轨迹方程.……………………4分
(2)方法1:如图,由题意知直线.files/image247.gif) 的斜率存在,
的斜率存在,
设.files/image247.gif) 的方程为
的方程为.files/image534.gif) (
(.files/image536.gif) ) …… ①…………………………………5分
) …… ①…………………………………5分
将①代入.files/image538.gif) ,
,
得.files/image540.gif) ,
,
………………6分
由.files/image542.gif) ,解得
,解得.files/image544.gif) .…………………………………………………………7分
.…………………………………………………………7分
设.files/image546.gif) ,
,.files/image548.gif) ,则
,则.files/image550.gif) …… ② ……………………8分
…… ② ……………………8分
令.files/image552.gif) ,则
,则.files/image554.gif) ,即
,即.files/image556.gif) ,即
,即.files/image558.gif) ,且
,且.files/image560.gif)
……………………9分
由②得,.files/image562.gif)
即.files/image564.gif)
.files/image566.gif) .……………………………………………11分
.……………………………………………11分
.files/image568.gif) 且
且.files/image570.gif)
.files/image572.gif) 且
且.files/image574.gif) .
.
解得.files/image576.gif) 且
且.files/image578.gif) ………………………………………………13分
………………………………………………13分
.files/image580.gif) ,
,.files/image582.gif) 且
且.files/image578.gif) .
.
∴△OBE与△OBF面积之比的取值范围是.files/image584.gif) .……………14分
.……………14分
方法2:如图,由题意知直线.files/image247.gif) 的斜率存在,
的斜率存在,
设.files/image247.gif) 的方程为
的方程为.files/image586.gif)
.files/image588.gif) …… ①…………5分
…… ①…………5分
将①代入.files/image538.gif) ,
,
整理,得.files/image590.gif) ,…………6分
,…………6分
由.files/image542.gif) ,解得
,解得.files/image592.gif) .………………………………………………………………7分
.………………………………………………………………7分
设.files/image546.gif) ,
,.files/image548.gif) ,则
,则.files/image594.gif) …… ② ……………………8分
…… ② ……………………8分
令.files/image596.gif) ,且
,且.files/image598.gif) .…………………………………9分
.…………………………………9分
将.files/image600.gif) 代入②,得
代入②,得.files/image602.gif)
∴.files/image604.gif) .即
.即.files/image606.gif) .……………………………………11分
.……………………………………11分
∵.files/image592.gif) 且
且.files/image609.gif) ,∴
,∴.files/image611.gif) 且
且.files/image613.gif) .
.
即.files/image615.gif) 且
且.files/image578.gif) .
.
解得.files/image576.gif) 且
且.files/image578.gif) .……………………………………………13分
.……………………………………………13分
.files/image580.gif) ,
,.files/image582.gif) 且
且.files/image578.gif) .
.
故△OBE与△OBF面积之比的取值范围是.files/image584.gif) .……………14分
.……………14分
21.(本小题满分14分)
(本小题主要考查等差数列、不等式及其性质等基础知识,考查分类讨论、化归与转化的数学思想方法,以及抽象概括能力、运算求解能力)
解:(1)由已知,.files/image618.gif) (
(.files/image272.gif) ,
,.files/image274.gif) ), …………………2分
), …………………2分
即.files/image620.gif) (
(.files/image272.gif) ,
,.files/image274.gif) ),且
),且.files/image622.gif) .
.
∴数列.files/image261.gif) 是以
是以.files/image263.gif) 为首项,公差为1的等差数列.
为首项,公差为1的等差数列.
∴.files/image625.gif) .……………………………………………………………………………4分
.……………………………………………………………………………4分
(2)∵.files/image625.gif) ,∴
,∴.files/image628.gif) ,要使
,要使.files/image280.gif) 恒成立,
恒成立,
∴.files/image630.gif) 恒成立,
恒成立,
∴.files/image632.gif) 恒成立,
恒成立,
∴.files/image634.gif) 恒成立.……………………………………………………………6分
恒成立.……………………………………………………………6分
(?)当.files/image012.gif) 为奇数时,即
为奇数时,即.files/image637.gif) 恒成立,…………………………………………7分
恒成立,…………………………………………7分
当且仅当.files/image639.gif) 时,
时,.files/image641.gif) 有最小值为1,
有最小值为1,
∴.files/image643.gif) .………………………………………………………………………………9分
.………………………………………………………………………………9分
(?)当.files/image012.gif) 为偶数时,即
为偶数时,即.files/image646.gif) 恒成立,………………………………………10分
恒成立,………………………………………10分
当且仅当.files/image648.gif) 时,
时,.files/image650.gif) 有最大值
有最大值.files/image652.gif) ,
,
∴.files/image654.gif) .……………………………………………………………………………12分
.……………………………………………………………………………12分
即.files/image656.gif) ,又
,又.files/image278.gif) 为非零整数,则
为非零整数,则.files/image659.gif) .
.
综上所述,存在.files/image659.gif) ,使得对任意
,使得对任意.files/image274.gif) ,都有
,都有.files/image662.gif) .…………………14分
.…………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com