
题目列表(包括答案和解析)
在四面体ABCD中,DA⊥面ABC,∠ABC=90°,AE⊥CD,AF⊥DB.求证:
(1)EF⊥DC; (2)平面DBC⊥平面AEF; (3)若AD=AB=a,AC=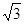 求二面角B-DC-A的正弦值。
求二面角B-DC-A的正弦值。
(本小题满分12分)如图,四棱锥P-ABCD的底面ABCD是直角梯形,∠DAB=∠ABC=90o,PA⊥底面ABCD,PA=AB=AD=2,BC=1,E为PD的中点.

(1) 求证:CE∥平面PAB;
(2) 求PA与平面ACE所成角的大小;
(3) 求二面角E-AC-D的大小.
一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,
 ∠ABC=45°,AB=AD=1,DC⊥BC,这个平面图形的面积为______
∠ABC=45°,AB=AD=1,DC⊥BC,这个平面图形的面积为______
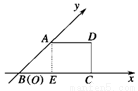
在△ABC中,AB=2,BC=1.5,∠ABC=120°,若使△ABC绕直线 旋转一周,则所形成的几何体的体积是( ).
旋转一周,则所形成的几何体的体积是( ).
A.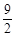 π B.
π B. π C.
π C.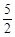 π D.
π D.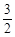 π
π
((本小题满分12分)
如图,已知四棱锥P—ABCD的底面是直角梯形,∠ABC=∠BCD=90o,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.
(1)求证:PA⊥BD;
(2)求二面角P—DC—B的大小.
一.选择题:(本大共12小题,每小题5分,在每小题的四个选项中只有一个是正确的.)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
D
C
D
A
B
C
B
C
A
D
二、填空题(本大题4个小题,每小题4分,共16分,只填结果,不要过程)
13、 3 14、 9
15、
240
16、

三.解答题(本大题共6个小题,共74分,解答应写出文字说明、证明过程或演算步骤。)
17、证明:(1)连结 ,设
,设
连结 ,
,
 是正方体
是正方体  是平行四边形
是平行四边形
 ∥
∥ 且
且  2分
2分
又 分别是
分别是 的中点,
的中点, ∥
∥ 且
且
 是平行四边形
4分
是平行四边形
4分
 ∥
∥ 面
面 ,
, 面
面

 ∥面
∥面 6分
6分
(2) 面
面
 7分
7分
又 ,
, 
 9分
9分
同理可证 ,
11分
,
11分
又

 面
面 12分
12分
18.解:(1) =3125;------4分(2)A
=3125;------4分(2)A =120; ------8分(3)
=120; ------8分(3) =1200-----12分.
=1200-----12分.
平面 平面
平面 -----------------------------------------------------6分
-----------------------------------------------------6分
 (2)ABCD为菱形,
(2)ABCD为菱形, ,过O在平面OEB内作OF
,过O在平面OEB内作OF BE于F,连OF,
BE于F,连OF,  AFO为二面角
AFO为二面角 的平面角, tan
的平面角, tan AFO = -------12分
AFO = -------12分
20.(1) ---------4分
---------4分
 .(2)
.(2)  ---------8分
---------8分
.(3)  ---------12分
---------12分
21.解:(1)过A作BC的反向延长线的垂线,交于点E,连ED,
∵面ACB⊥面BCD,∴AE⊥面BCD 又AB=BC=BD,
∠ABC=∠DBC=1200
 ∴AE=ED=
∴∠ADE=
∴AE=ED=
∴∠ADE= ----------4分
----------4分
(2)过D作EC的平行线与过C平行于ED的直线交于F。
由(1)知,EDFC为矩形 ∵DF⊥DE, ∴DF⊥AD,即BC⊥AD ∴ 900-即为所求 ----8分

 (3)过E作EG⊥BD于G,连结AG
(3)过E作EG⊥BD于G,连结AG
由三垂线定理知,AG⊥BD。由 ,
在Rt△AEG中,tan∠AGE=2, ∠AGE=arctan2
∴二面角A―BD―C的度数为 π-arctan2 - -------12分
22. (1)∵B1D⊥面ABC ∴B1D⊥AC
又∵AC⊥BC 且B1D∩BC=D
∴ 平面
平面 -------4分
-------4分
(2)连结B 平面
平面

∴B 是菱形 ---------6分
是菱形 ---------6分
∵B1D⊥BC 且D为 的中点 ∴B
的中点 ∴B =
= ------9分
------9分
 (3)过C1在平面
(3)过C1在平面 内作C1O∥B1D,交BC的延长线于O点,
内作C1O∥B1D,交BC的延长线于O点,
过O作OM⊥AB于M点,连结C ,∴C
,∴C
∴∠OMC1是二面角 的平面角---------11分
的平面角---------11分
设 =
=
∴BD=a , C1O= B1D= a , BO=
a , BO=
∵∠CBA= , ∴OM=
, ∴OM= a =B1D , ∴∠OMC1=
a =B1D , ∴∠OMC1=
∴二面角 的大小为
的大小为 ---------14分
---------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com