题目列表(包括答案和解析)
（2012•安徽模拟）为了了解某校高三文科学生在皖南八校第二次联考的数学成绩，从全校400名文科学生成绩中抽取了 40名学生的成绩，将所得数据整理后，画出其频率分布直方图（如图）．已知第一组与第六组的频数和为6，并且从左到右各长方形髙的比为 m：3：5：6：3：1．
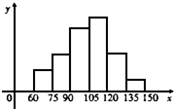
为了了解某校高三文科学生在皖南八校第二次联考的数学成绩，从全校400名文科学生成绩中抽取了 40名学生的成绩，将所得数据整理后，画出其频率分布直方图（如图）．已知第一组与第六组的频数和为6，并且从左到右各长方形髙的比为 m：3：5：6：3：1．| 1 |
| x |
| 1 |
| x2 |
一、选择题
1. C 2. A 3. C 4. D 5.D 6. B 7. C 8. B
二、填空题
9.
，
10.
11.
12.
13. ①③ 14.（1，2）
三、解答题
15. 解：
1分
2分
???3分
（Ⅰ）
的最小正周期为
； ???6分
（Ⅱ）由
， 
7分
得
，
8分
的单调增区间为
???9分
（Ⅲ）因为
，即
10分
11分
???12分
16.解：(Ⅰ)∵
∴当
时，则
得
1分
解得
???3分
当
时，则由
4分
解得
??6分
(Ⅱ) 当
时，
???7分
???8分
，
中各项不为零
???9分
???10分
是以
为首项，为公比的数列
???11分
???12分
17.
(Ⅰ) 证明：∵
，
∴ 令
，得
???1分
∴
???2分
令
，得
???3分
即
∴函数为奇函数
???4分
(Ⅱ) 证明：设
，且
???5分
则 
???6分
又∵当
时
∴
???7分
即
???8分
∴函数在
上是增函数
???9分
(Ⅲ) ∵函数在上是增函数
∴函数在区间［－4，4］上也是增函数
???10分
∴函数的最大值为
，最小值为
???11分
∵
∴
???12分
∵函数为奇函数
∴
???13分
故，函数的最大值为12，最小值为
.
???14分
18. 解：设甲现在所在位置为A，乙现在所在位置为B，运动t秒后分别到达位置C、D,如图可知CD即为甲乙的距离.
??1分
当
时,
??2分
??3分
??5分
时，
??7分
当
时,C、B重合, 
??9分
当
时,
??10分
??12分
??13分
综上所述：经过2秒后两人距离最近为
. ??14分
19. 解证：（I）易得
???1分
的两个极值点
的两个实根，又
???3分
∴
???5分
∵
???6分
???8分
（Ⅱ）设
则
???10分
由
???11分
上单调递减
???12分
???13分
∴
的最大值是 
???14分
20.解：(Ⅰ)当时，
， 
，???1分
数列
为等比数列，
，故
???2分
???3分
(Ⅱ)设数列
公差
，
根据题意有：
，
???4分
即：
，
，代入上式有： ???5分
,
???7分
即关于不等式
有解
???8分
当
时，
???9分
???10分
(Ⅲ)
，记
前n项和为
???11分
???12分
???13分
???14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com