
题目列表(包括答案和解析)
| 1 |
| 2 |
| AB |
| AC |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 2 |
| 1 |
| 3 |
| π |
| 2 |
设 ,
, .
.
(Ⅰ)证明: ;
;
(Ⅱ)求证:在数轴上, 介于
介于 与
与 之间,且距
之间,且距 较远;
较远;
(Ⅲ)在数轴上, 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,
说明理由.
设 ,
, .
.
(Ⅰ)证明: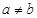 ;
;
(Ⅱ)求证:在数轴上,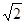 介于
介于 与
与 之间,且距
之间,且距 较远;
较远;
(Ⅲ)在数轴上, 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,
说明理由.
 ,
, .
. ;
; 介于
介于 与
与 之间,且距
之间,且距 较远;
较远; 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,一、选择题(本大题8小题,共40分,每小题给出的四个选项中,只有一项是符合要求)
题号
1
2
3
4
5
6
7
8
答案
A
C
A
D
A
B
B
B
二、填空题:(本大题共须作6小题,每小题5分,共30分,把答案填写在题横线上).
9、 试题及答案.files/image134.gif) 10、
10、试题及答案.files/image136.gif) 11、
11、试题及答案.files/image138.gif) 12、3
12、3
▲选做题:在下面三道题中选做两题,三题都选的只计算前两题的得分。
13、3
;14、试题及答案.files/image140.gif) 。 ; 15、
。 ; 15、试题及答案.files/image142.gif)
三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤)
16、(本小题满分14分)解:(1)试题及答案.files/image079.gif) 的内角和
的内角和试题及答案.files/image144.gif)
试题及答案.files/image146.gif)
试题及答案.files/image081.gif)
试题及答案.files/image148.gif) …………………1分
…………………1分
试题及答案.files/image150.gif)
试题及答案.files/image152.gif) ……………5分
……………5分
试题及答案.files/image154.gif)
试题及答案.files/image156.gif) …………………7分
…………………7分
(2)试题及答案.files/image158.gif)
试题及答案.files/image160.gif) ……………9分
……………9分
试题及答案.files/image162.gif)
试题及答案.files/image164.gif) …………12分
…………12分
当试题及答案.files/image166.gif) 即
即试题及答案.files/image168.gif) 时,y取得最大值
时,y取得最大值试题及答案.files/image170.gif) ………………………14分
………………………14分
17.(本小题满分12分)
解:(1)3个旅游团选择3条不同线路的概率为:P1=试题及答案.files/image172.gif) …………3分
…………3分
(2)恰有两条线路没有被选择的概率为:P2=试题及答案.files/image174.gif) ……6分
……6分
(3)设选择甲线路旅游团数为ξ,则ξ=0,1,2,3………………7分
P(ξ=0)=试题及答案.files/image176.gif) P(ξ=1)=
P(ξ=1)=试题及答案.files/image178.gif)
P(ξ=2)= 试题及答案.files/image180.gif) P(ξ=3)=
P(ξ=3)= 试题及答案.files/image182.gif) ………………9分
………………9分
∴ξ的分布列为:
ξ
0
1
2
3
试题及答案.files/image184.gif)
试题及答案.files/image184.gif)
试题及答案.files/image187.gif)
试题及答案.files/image189.gif)
………………10分
∴期望Eξ=0×试题及答案.files/image184.gif) +1×
+1×试题及答案.files/image184.gif) +2×
+2×试题及答案.files/image187.gif) +3×
+3×试题及答案.files/image189.gif) =
=试题及答案.files/image191.gif) ………………12分
………………12分
18.(本小题满分12分)
|