
题目列表(包括答案和解析)
在平面直角坐标系中,已知点![]() 、
、![]() ,
,![]() 是平面内一动点,直线
是平面内一动点,直线![]() 、
、![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
| 1 |
| 2 |
| e |
| 1 |
| 2 |
| OC |
| OA |
| OB |
| BM |
| e |
| CM |
| AB |
在平面直角坐标系中,已知点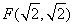 及直线
及直线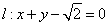 ,曲线
,曲线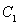 是满足下列两个条件的动点
是满足下列两个条件的动点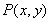 的轨迹:①
的轨迹:①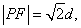 其中
其中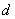 是
是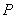 到直线
到直线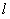 的距离;②
的距离;②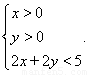
(1) 求曲线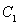 的方程;
的方程;
(2) 若存在直线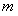 与曲线
与曲线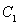 、椭圆
、椭圆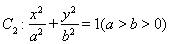 均相切于同一点,求椭圆
均相切于同一点,求椭圆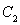 离心率
离心率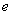 的取值范围.
的取值范围.
在平面直角坐标系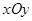 中,已知点
中,已知点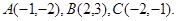
(1)求以线段AB、AC为邻边的平行四边形的两条对角线的长;
(2)设实数t满足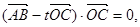 求t的值。
求t的值。
一、 选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个备选项中,有且只有一项是符合要求的.
题号
1
2
3
4
5
6
7
8
答案
D
A
A
C
B
B
C
A
二、 填空题:本大题共7小题,每小题5分,共30分.其中13~15小题是选做题,考生只能选做两题,若三题全答,则只计算前两题得分.
9.试题.files/image368.gif) 10.
10.试题.files/image370.gif) 11.
11.试题.files/image372.gif)
12.②③ 13.试题.files/image374.gif) ,
,试题.files/image376.gif)
14.试题.files/image378.gif) ,
,试题.files/image057.gif) 15.
15.试题.files/image381.gif) ,
,试题.files/image383.gif)
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
16. 解:(Ⅰ)因为试题.files/image216.gif) ,
,试题.files/image218.gif) ,所以
,所以
试题.files/image385.gif)
试题.files/image387.gif) .
.
因此,当试题.files/image389.gif) ,即
,即试题.files/image391.gif) (
(试题.files/image393.gif) )时,
)时,试题.files/image033.gif) 取得最大值
取得最大值试题.files/image396.gif) ;
;
(Ⅱ)由试题.files/image398.gif) 及
及试题.files/image224.gif) 得
得试题.files/image401.gif) ,两边平方得
,两边平方得
试题.files/image403.gif) ,即
,即试题.files/image405.gif) .
.
因此,试题.files/image407.gif) .
.
17. 解:(Ⅰ)记“小球落入试题.files/image117.gif) 袋中”为事件
袋中”为事件试题.files/image117.gif) ,“小球落入
,“小球落入试题.files/image119.gif) 袋中”为事件
袋中”为事件试题.files/image119.gif) ,则事件
,则事件试题.files/image117.gif) 的对立事件为
的对立事件为试题.files/image119.gif) ,而小球落入
,而小球落入试题.files/image119.gif) 袋中当且仅当小球一直向左落下或一直向右落下,故
袋中当且仅当小球一直向左落下或一直向右落下,故
试题.files/image415.gif) ,
,
从而试题.files/image417.gif) ;
;
(Ⅱ)显然,随机变量试题.files/image419.gif) ,故
,故
试题.files/image421.gif) ,
,
试题.files/image423.gif) .
.
18. 试题.files/image425.gif) 解: 建立如图所示的空间直角坐标系,
解: 建立如图所示的空间直角坐标系,
并设试题.files/image427.gif) ,则
,则
(Ⅰ)试题.files/image429.gif) ,
,试题.files/image431.gif) ,
,
所以试题.files/image433.gif) ,从而得
,从而得
试题.files/image262.gif) ;
;
(Ⅱ)设试题.files/image436.gif) 是平面
是平面试题.files/image438.gif) 的
的
法向量,则由试题.files/image440.gif) ,
,试题.files/image442.gif) 及
及
试题.files/image429.gif) ,
,试题.files/image444.gif)
得
试题.files/image446.gif) 可以取
可以取试题.files/image448.gif) .
.
显然,试题.files/image450.gif) 为平面
为平面试题.files/image452.gif) 的法向量.
的法向量.
设二面角试题.files/image264.gif) 的平面角为
的平面角为试题.files/image455.gif) ,则此二面角的余弦值
,则此二面角的余弦值
试题.files/image457.gif) .
.
19. 解:(Ⅰ)依题意,有试题.files/image459.gif) (
(试题.files/image461.gif) ),化简得
),化简得
试题.files/image463.gif) (
(试题.files/image461.gif) ),
),
这就是动点试题.files/image099.gif) 的轨迹
的轨迹试题.files/image279.gif) 的方程;
的方程;
(Ⅱ)依题意,可设试题.files/image467.gif) 、
、试题.files/image469.gif) 、
、试题.files/image471.gif) ,则有
,则有
试题.files/image473.gif) ,
,
两式相减,得试题.files/image475.gif) ,由此得点
,由此得点试题.files/image258.gif) 的轨迹方程为
的轨迹方程为
试题.files/image478.gif) (
(试题.files/image480.gif) ).
).
设直线试题.files/image292.gif) :
:试题.files/image483.gif) (其中
(其中试题.files/image485.gif) ),则
),则
试题.files/image487.gif) ,
,
故由试题.files/image489.gif) ,即
,即试题.files/image491.gif) ,解之得
,解之得试题.files/image294.gif) 的取值范围是
的取值范围是试题.files/image494.gif) .
.
20. 解:(Ⅰ)依题意知:直线试题.files/image283.gif) 是函数
是函数试题.files/image296.gif) 在点
在点试题.files/image374.gif) 处的切线,故其斜率
处的切线,故其斜率
试题.files/image499.gif) ,
,
所以直线试题.files/image283.gif) 的方程为
的方程为试题.files/image502.gif) .
.
又因为直线试题.files/image283.gif) 与
与试题.files/image304.gif) 的图像相切,所以由
的图像相切,所以由
试题.files/image506.gif) ,
,
得试题.files/image508.gif) (
(试题.files/image510.gif) 不合题意,舍去);
不合题意,舍去);
(Ⅱ)因为试题.files/image512.gif) (
(试题.files/image514.gif) ),所以
),所以
试题.files/image516.gif) .
.
当试题.files/image518.gif) 时,
时,试题.files/image520.gif) ;当
;当试题.files/image037.gif) 时,
时,试题.files/image523.gif) .
.
因此,试题.files/image314.gif) 在
在试题.files/image526.gif) 上单调递增,在
上单调递增,在试题.files/image528.gif) 上单调递减.
上单调递减.
因此,当试题.files/image530.gif) 时,
时,试题.files/image314.gif) 取得最大值
取得最大值试题.files/image533.gif) ;
;
(Ⅲ)当试题.files/image316.gif) 时,
时,试题.files/image536.gif) .由(Ⅱ)知:当
.由(Ⅱ)知:当试题.files/image518.gif) 时,
时,试题.files/image539.gif) ,即
,即试题.files/image541.gif) .因此,有
.因此,有
试题.files/image543.gif) .
.
21. 解:(Ⅰ)试题.files/image545.gif) ,
,试题.files/image547.gif) ,
,试题.files/image549.gif) ;
;
(Ⅱ)依题意,得试题.files/image551.gif) ,
,试题.files/image553.gif) ,由此及
,由此及试题.files/image555.gif) 得
得
试题.files/image557.gif) ,
,
即试题.files/image559.gif) .
.
由(Ⅰ)可猜想:试题.files/image561.gif) (
(试题.files/image352.gif) ).
).
下面用数学归纳法予以证明:
(1)当试题.files/image564.gif) 时,命题显然成立;
时,命题显然成立;
(2)假定当试题.files/image566.gif) 时命题成立,即有
时命题成立,即有试题.files/image568.gif) ,则当
,则当试题.files/image570.gif) 时,由归纳假设及
时,由归纳假设及
试题.files/image572.gif)
得试题.files/image574.gif) ,即
,即
试题.files/image576.gif) ,
,
解之得
试题.files/image578.gif) (
(试题.files/image580.gif) 不合题意,舍去),
不合题意,舍去),
即当试题.files/image570.gif) 时,命题成立.
时,命题成立.
由(1)、(2)知:命题成立.
(Ⅲ)试题.files/image357.gif)
试题.files/image583.gif)
试题.files/image585.gif) .
.
令试题.files/image587.gif) (
(试题.files/image589.gif) ),则
),则试题.files/image591.gif) ,所以
,所以试题.files/image033.gif) 在
在试题.files/image594.gif) 上是增函数,故当
上是增函数,故当试题.files/image596.gif) 时,
时,试题.files/image033.gif) 取得最小值
取得最小值试题.files/image057.gif) ,即当
,即当试题.files/image564.gif) 时,
时,试题.files/image601.gif) .
.
试题.files/image362.gif) (
(试题.files/image603.gif) ,
,试题.files/image605.gif) )
)
试题.files/image607.gif) ,即
,即试题.files/image609.gif) (
(试题.files/image605.gif) )
)
试题.files/image611.gif) .
.
解之得,实数试题.files/image364.gif) 的取值范围为
的取值范围为试题.files/image614.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com