
题目列表(包括答案和解析)
15.解:根据条件去画满足条件的二次函数图象就可判断出
某大型超市为促销商品,特举办“购物摇奖100%中奖”活动,凡消费者在该超市购物满20元,享受一次摇奖机会,购物满40元,享受两次摇奖机会,依次类推。摇奖机的旋转圆盘是均匀的,扇形区域A、B、C、D、E所对应的圆心角的比值分别为1:2:3:4:5。相应区域分别设立一、二、三、四、五等奖,奖金分别为5元、4元、3元、2元、1元。求某人购物30元,获得奖金的分布列.
 三棱锥A-BCD中,对棱AD、BC所成的角为30°且AD=BC=a.截面EFGH是平行四边形,交AB、AC、CD、BD于E、F、G、H,设
三棱锥A-BCD中,对棱AD、BC所成的角为30°且AD=BC=a.截面EFGH是平行四边形,交AB、AC、CD、BD于E、F、G、H,设| BE | AB |
三棱柱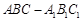 中,侧棱与底面垂直,
中,侧棱与底面垂直,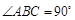 ,
,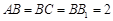 ,
,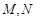 分别是
分别是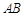 ,
, 的中点.
的中点.
(Ⅰ)求证: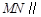 平面
平面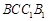 ;
;
(Ⅱ)求证: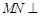 平面
平面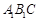 ;
;
(Ⅲ)求三棱锥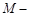
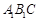 的体积.
的体积.
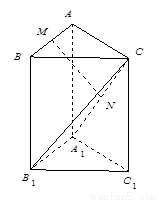
【解析】第一问利连结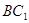 ,
,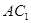 ,∵M,N是AB,
,∵M,N是AB, 的中点∴MN//
的中点∴MN//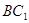 .
.
又∵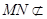 平面
平面 ,∴MN//平面
,∴MN//平面 .
. ----------4分
----------4分
⑵中年∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,∴四边形 是正方形.∴
是正方形.∴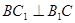 .∴
.∴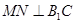 .连结
.连结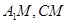 ,
,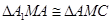 .
.
∴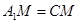 ,又N中
,又N中 的中点,∴
的中点,∴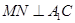 .
.
∵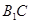 与
与 相交于点C,∴MN
相交于点C,∴MN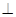 平面
平面 . --------------9分
. --------------9分
⑶中由⑵知MN是三棱锥M- 的高.在直角
的高.在直角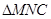 中,
中,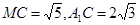 ,
,
∴MN=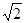 .又
.又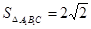 .
.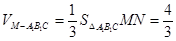 .得到结论。
.得到结论。
⑴连结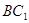 ,
,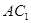 ,∵M,N是AB,
,∵M,N是AB, 的中点∴MN//
的中点∴MN//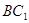 .
.
又∵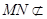 平面
平面 ,∴MN//平面
,∴MN//平面 .
. --------4分
--------4分
⑵∵三棱柱ABC-A1B1C1中,侧棱与底面垂直,
∴四边形 是正方形.∴
是正方形.∴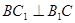 .
.
∴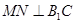 .连结
.连结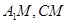 ,
,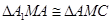 .
.
∴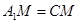 ,又N中
,又N中 的中点,∴
的中点,∴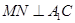 .
.
∵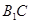 与
与 相交于点C,∴MN
相交于点C,∴MN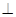 平面
平面 . --------------9分
. --------------9分
⑶由⑵知MN是三棱锥M- 的高.在直角
的高.在直角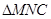 中,
中,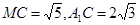 ,
,
∴MN=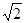 .又
.又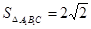 .
.
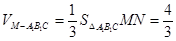
三.解答题:本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17. (本题满分10分)
已知函数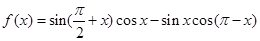 ,
,
(1)求函数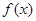 的最小正周期;
的最小正周期;
(2)在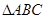 中,已知
中,已知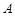 为锐角,
为锐角,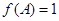 ,
,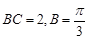 ,求
,求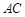 边的长.
边的长.
三、解答题:(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤.)
16. (本小题满分12分)
已知向量 ,定义函数
,定义函数
(Ⅰ)求函数 最小正周期;
最小正周期;
(Ⅱ)在△ABC中,角A为锐角,且 ,求边AC的长.
,求边AC的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com