
题目列表(包括答案和解析)
从集合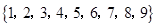 中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 .
中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 .
从集合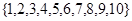 中任取三个不同的元素作为直线
中任取三个不同的元素作为直线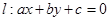 中
中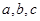 的值,若直线
的值,若直线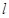 倾斜角小于
倾斜角小于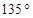 ,且
,且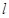 在
在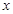 轴上的截距小于
轴上的截距小于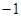 ,那么不同的直线
,那么不同的直线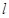 条数有
条数有
A、109条 B、110条 C、111条 D、120条
从集合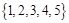 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组 ,规定
,规定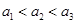 .
.
(1)从所有的三元有序数组中任选一个,求它的所有元素之和等于10的概率
(2)定义三元有序数组 的“项标距离”为
的“项标距离”为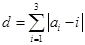 (其中
(其中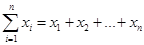 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
从集合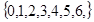 中任取两个互不相同的数
中任取两个互不相同的数 组成复数
组成复数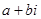 ,其中虚数有( )
,其中虚数有( )
A、30个 B、42 个 C、36 个 D、35个
从集合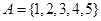 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组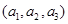 ,规定
,规定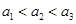
(1)从所有三元有序数组中任选一个,求它的所有元素之和等于10的概率;
(2)定义三元有序数组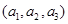 的“项标距离”为
的“项标距离”为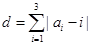 ,(其中
,(其中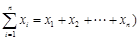 ,从所有三元有序数组中任选一个,求它的“项标距离”
,从所有三元有序数组中任选一个,求它的“项标距离”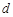 为偶数的概率;
为偶数的概率;
一、选择题:(每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
C
A
B
C
D
C
B
C
B
A
二、填空题:(每小题5分,共20分)
13、 0.1; 14、__(0,1]_; 15、---理科数学.files/image276.gif) ; 16、①④ ;
; 16、①④ ;
三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17. (1)由---理科数学.files/image278.gif) 得:
得:---理科数学.files/image280.gif) , ……………………………… 2分
, ……………………………… 2分
即---理科数学.files/image282.gif) ,
,---理科数学.files/image284.gif) ……………… 4分
……………… 4分
当---理科数学.files/image286.gif) 时,
时,---理科数学.files/image288.gif) ,
,---理科数学.files/image290.gif)
因为---理科数学.files/image292.gif) ,有
,有---理科数学.files/image294.gif) ,
,---理科数学.files/image296.gif) ,得
,得---理科数学.files/image298.gif)
故---理科数学.files/image300.gif) …………………………… 7分
…………………………… 7分
(2)∵---理科数学.files/image302.gif) 是奇函数,且将
是奇函数,且将---理科数学.files/image204.gif) 的图象先向右平移
的图象先向右平移---理科数学.files/image305.gif) 个单位,再向上平移1个单位,可以得到
个单位,再向上平移1个单位,可以得到---理科数学.files/image307.gif) 的图象,∴
的图象,∴---理科数学.files/image309.gif) 是满足条件的一个平移向量.……10分
是满足条件的一个平移向量.……10分
18. (Ⅰ)---理科数学.files/image311.gif) ,
,---理科数学.files/image313.gif) ……5分
……5分
(Ⅱ)---理科数学.files/image315.gif) ,
,---理科数学.files/image317.gif) ……8分
……8分
---理科数学.files/image319.gif) ,
,---理科数学.files/image321.gif) ……10分
……10分
19.
(Ⅰ) ---理科数学.files/image093.gif) ,
,---理科数学.files/image038.gif) 的可能取值为1,2,3
的可能取值为1,2,3
∴---理科数学.files/image323.gif) ∴
∴---理科数学.files/image325.gif) ,因此,随机变量
,因此,随机变量---理科数学.files/image152.gif) 的最大值为3
的最大值为3
---理科数学.files/image327.gif)
---理科数学.files/image329.gif) ……5分
……5分
(Ⅱ)---理科数学.files/image152.gif) 的可能取值为0,1,2,3,则……6分
的可能取值为0,1,2,3,则……6分
---理科数学.files/image331.gif) ,
,---理科数学.files/image333.gif) ,
,---理科数学.files/image335.gif) ,
,---理科数学.files/image337.gif) ……9分
……9分
随机变量---理科数学.files/image152.gif) 的分布列(略)
的分布列(略)
---理科数学.files/image339.gif) ……10分
……10分
20.(Ⅰ) 解法一:
---理科数学.files/image341.jpg)
(Ⅰ)证:由已知DF∥AB且---理科数学.files/image242.gif) DAD为直角,故ABFD是矩形,从而CD
DAD为直角,故ABFD是矩形,从而CD---理科数学.files/image240.gif) BF. ………..4分
BF. ………..4分
又PA---理科数学.files/image240.gif) 底面ABCD,CD
底面ABCD,CD---理科数学.files/image240.gif) AD,故知CD
AD,故知CD---理科数学.files/image240.gif) PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD
PD.在△PDC中,E、F分别PC、CD的中点,故EF∥PD,从而CD---理科数学.files/image240.gif) EF,由此得CD
EF,由此得CD---理科数学.files/image240.gif) 面BEF. ………..7分
面BEF. ………..7分
(Ⅱ)连结AC交BF于G.易知G为AC的中点.连接EG,则在△PAC中易知EC∥PA.又因
PA---理科数学.files/image240.gif) 底面ABCD,故BC
底面ABCD,故BC---理科数学.files/image240.gif) 底面ABCD.在底面ABCD中,过C作GH
底面ABCD.在底面ABCD中,过C作GH---理科数学.files/image240.gif) BD,垂足为H,连接EH.由三垂线定理知EH
BD,垂足为H,连接EH.由三垂线定理知EH---理科数学.files/image240.gif) BD.从而
BD.从而---理科数学.files/image242.gif) EHG为二面角E-BD-C的平面角. ………..10分
EHG为二面角E-BD-C的平面角. ………..10分
---理科数学.files/image343.jpg) 设AB=a,则在△PAC中,有
设AB=a,则在△PAC中,有
BG=---理科数学.files/image345.gif) PA=
PA=---理科数学.files/image345.gif) ka.
ka.
以下计算GH,考察底面的平面图(如答(19)图2).连结GD.
因S△CBD=---理科数学.files/image345.gif) BD?GH=
BD?GH=---理科数学.files/image345.gif) GB?OF.故GH=
GB?OF.故GH=---理科数学.files/image347.gif) .
.
在△ABD中,因为AB=a,AD=---理科数学.files/image349.gif) a
a
而GB=---理科数学.files/image345.gif) FB=
FB=---理科数学.files/image345.gif) AD-a.DF-AB,从而得GH=
AD-a.DF-AB,从而得GH=---理科数学.files/image347.gif) =
=
---理科数学.files/image351.gif) =
=---理科数学.files/image353.gif) 因此tanEHG=
因此tanEHG=---理科数学.files/image355.gif) =
=---理科数学.files/image357.gif) ………..12分
………..12分
由k>0知---理科数学.files/image359.gif) 是锐角,故要使
是锐角,故要使---理科数学.files/image359.gif) >
>---理科数学.files/image244.gif) ,必须
,必须---理科数学.files/image362.gif) >tan
>tan---理科数学.files/image244.gif) =
=---理科数学.files/image364.gif)
解之得,k的取值范围为k>---理科数学.files/image366.gif) ………..14分
………..14分
解法二:
(Ⅰ)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为:轴建立空间直角坐标系,设AB=a,则易知点A,B,C,D,F的坐标分别为
---理科数学.files/image368.jpg) A(0,0,0),B(a,0,0),C(
A(0,0,0),B(a,0,0),C(
F(a,
从而---理科数学.files/image370.gif) =(
=(---理科数学.files/image372.gif) =(0,
=(0,
---理科数学.files/image370.gif) ?
?---理科数学.files/image372.gif) =0,故
=0,故---理科数学.files/image370.gif)
---理科数学.files/image240.gif)
---理科数学.files/image372.gif) .
.
设PA=b,则P(0,0,b),而E为PC中点.故 第(20)
---理科数学.files/image370.gif) ?
?---理科数学.files/image376.gif) =0,故
=0,故---理科数学.files/image370.gif)
---理科数学.files/image240.gif)
---理科数学.files/image376.gif) .
.
由此得CD---理科数学.files/image240.gif) 面BEF.
面BEF.
(Ⅱ)设E在xOy平面上的投影为G,过G作GH---理科数学.files/image240.gif) BD垂足为H,由三垂线定理知EH
BD垂足为H,由三垂线定理知EH---理科数学.files/image240.gif) BD.
BD.
从而---理科数学.files/image242.gif) EHG为二面角E-BD-C的平面角.
EHG为二面角E-BD-C的平面角.
由PA=k?AB得P(0,0,ka),E---理科数学.files/image383.gif) ,G(a,a,0).设H(x,y,0),则
,G(a,a,0).设H(x,y,0),则---理科数学.files/image385.gif) =(x-a,y-a,0),
=(x-a,y-a,0), ---理科数学.files/image387.gif) =(-a,
=(-a,
由---理科数学.files/image385.gif) ?
?---理科数学.files/image387.gif) =0得=a(x-a)+
=0得=a(x-a)+
又因---理科数学.files/image389.gif) =(x,a,y,0),且
=(x,a,y,0),且---理科数学.files/image389.gif) 与
与---理科数学.files/image387.gif) 的方向相同,故
的方向相同,故---理科数学.files/image392.gif) =
=---理科数学.files/image394.gif) ,即2x+y=
,即2x+y=
由①②解得x=---理科数学.files/image396.gif) a,y=
a,y=---理科数学.files/image398.gif) a,从而
a,从而---理科数学.files/image385.gif) =
=---理科数学.files/image400.gif) ,|
,|---理科数学.files/image385.gif) |=
|=---理科数学.files/image402.gif) a.
a.
tanEHG=---理科数学.files/image404.gif) =
=---理科数学.files/image406.gif) =
=---理科数学.files/image362.gif) .由k>0知,EHC是锐角,由
.由k>0知,EHC是锐角,由---理科数学.files/image242.gif) EHC>
EHC>---理科数学.files/image409.gif) 得tanEHG>tan
得tanEHG>tan---理科数学.files/image409.gif) 即
即---理科数学.files/image362.gif) >
>---理科数学.files/image411.gif) 故k的取值范围为k>
故k的取值范围为k>---理科数学.files/image413.gif) .
.
21.解:(1)由---理科数学.files/image415.gif)
因直线---理科数学.files/image417.gif) 相切,
相切,---理科数学.files/image419.gif)
---理科数学.files/image421.gif) ,
,
∵椭圆---理科数学.files/image423.gif) 的两焦点与短轴的一个端点的连线构成等腰直角三角形,∴
的两焦点与短轴的一个端点的连线构成等腰直角三角形,∴---理科数学.files/image425.gif)
故所求椭圆方程为---理科数学.files/image427.gif) …………4分
…………4分
(2)当L与x轴平行时,以AB为直径的圆的方程:---理科数学.files/image429.gif)
当L与x轴平行时,以AB为直径的圆的方程:---理科数学.files/image431.gif)
由---理科数学.files/image433.gif)
即两圆相切于点(0,1)
因此,所求的点T如果存在,只能是(0,1)…………8分
事实上,点T(0,1)就是所求的点,证明如下.
当直线L垂直于x轴时,以AB为直径的圆过点T(0,1)
若直线L不垂直于x轴,可设直线L:---理科数学.files/image435.gif)
由---理科数学.files/image437.gif)
记点---理科数学.files/image439.gif) 、
、---理科数学.files/image441.gif)
---理科数学.files/image443.gif)
---理科数学.files/image445.gif)
---理科数学.files/image447.gif)
所以TA⊥TB,即以AB为直径的圆恒过点T(0,1)
所以在坐标平面上存在一个定点T(0,1)满足条件.…………12分
22.
解答:(1)---理科数学.files/image449.gif) ,由题意及导数的几何意义得
,由题意及导数的几何意义得
---理科数学.files/image451.gif) ,
,---理科数学.files/image453.gif) (1)
(1)
---理科数学.files/image455.gif) ,
(2) ……2分
,
(2) ……2分
又---理科数学.files/image457.gif) ,可得
,可得---理科数学.files/image459.gif) ,即
,即---理科数学.files/image461.gif) ,故
,故---理科数学.files/image463.gif)
由(1)得---理科数学.files/image465.gif) ,代入
,代入---理科数学.files/image457.gif) ,再由
,再由---理科数学.files/image468.gif) ,得
,得
---理科数学.files/image470.gif) ,
(3) ……4分
,
(3) ……4分
将---理科数学.files/image465.gif) 代入(2)得
代入(2)得---理科数学.files/image473.gif) ,即方程
,即方程---理科数学.files/image475.gif) 有实根.
有实根.
故其判别式---理科数学.files/image477.gif) 得
得---理科数学.files/image479.gif) ,或
,或---理科数学.files/image481.gif) , (4)
, (4)
由(3),(4)得---理科数学.files/image260.gif) ;……6分
;……6分
(2)由---理科数学.files/image449.gif) 的判别式
的判别式---理科数学.files/image484.gif) ,
,
知方程---理科数学.files/image486.gif) 有两个不等实根,设为
有两个不等实根,设为---理科数学.files/image488.gif) ,
,
又由---理科数学.files/image490.gif) 知,
知,---理科数学.files/image492.gif) 为方程(
为方程(---理科数学.files/image494.gif) )的一个实根,则有根与系数的关系得
)的一个实根,则有根与系数的关系得
---理科数学.files/image496.gif) , ……8分
, ……8分
当---理科数学.files/image498.gif) 或
或---理科数学.files/image500.gif) 时,
时,---理科数学.files/image502.gif) ,当
,当---理科数学.files/image504.gif) 时,
时,---理科数学.files/image506.gif) ,
,
故函数---理科数学.files/image204.gif) 的递增区间为
的递增区间为---理科数学.files/image509.gif) ,由题设知
,由题设知---理科数学.files/image511.gif) ,
,
因此---理科数学.files/image513.gif) ,由(Ⅰ)知
,由(Ⅰ)知---理科数学.files/image260.gif) 得
得---理科数学.files/image515.gif) 的取值范围为
的取值范围为---理科数学.files/image517.gif) ;……10分
;……10分
(3)由---理科数学.files/image273.gif) ,即
,即---理科数学.files/image519.gif) ,即
,即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com