练习册

  • 练习册
  • 试题
    17． 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分13分）有一问题，在半小时内，甲能解决它的概率是0.5，乙能解决它的概率是，

     如果两人都试图独立地在半小时内解决它，计算：w.w.w.k.s.5.u.c.o.m      

       （1）两人都未解决的概率；

       （2）问题得到解决的概率。

    查看答案和解析>>

    （本小题满分13分）  已知是等比数列, ；是等差数列, , .

    (1) 求数列、的通项公式；

    (2) 设+…+,…,其中,…试比较与的大小,并证明你的结论.

    查看答案和解析>>

    （本小题满分13分） 现有一批货物由海上从A地运往B地，已知货船的最大航行速度为35海里/小时，A地至B地之间的航行距离约为500海里，每小时的运输成本由燃料费和其余费用组成，轮船每小时的燃料费用与轮船速度的平方成正比（比例系数为0.6），其余费用为每小时960元.

    （1）把全程运输成本y(元)表示为速度x(海里/小时)的函数；

    （2）为了使全程运输成本最小，轮船应以多大速度行驶？

    查看答案和解析>>

    （本小题满分13分）

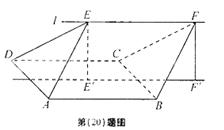
    如图，ABCD的边长为2的正方形，直线l与平面ABCD平行，g和F式l上的两个不同点，且EA=ED，FB=FC， 和是平面ABCD内的两点，和都与平面ABCD垂直，

    （Ⅰ）证明：直线垂直且平分线段AD：w.w.w.k.s.5.u.c.o.m       

    （Ⅱ）若∠EAD=∠EAB=60°，EF=2，求多面

    体ABCDEF的体积。

     

    查看答案和解析>>

    （本小题满分13分）两个人射击，甲射击一次中靶概率是p1，乙射击一次中靶概率是p2，已知 , 是方程x2－5x + 6 = 0的根，若两人各射击5次，甲的方差是 ．(1) 求 p1、p2的值；(2) 两人各射击2次，中靶至少3次就算完成目的，则完成目的的概率是多少？(3) 两人各射击一次，中靶至少一次就算完成目的，则完成目的的概率是多少？

    查看答案和解析>>

    一、选择题（每小题5分，共50分）

    1―5：ABCDC    6―10：BAAAD   

    二、填空题（每小题4分，共24分）

    11．；12．99；13．207；14．0；15．2；

    16．[1，2]或填[3，4]或填它们的任一子区间（答案有无数个）。

    三、解答题（共76分）

    17．（1）解：由

          有………………2分

          由，……………3分

          由余弦定理……5分

          当…………7分

       （2）由

          则，……………………9分

          由

          ……………………13分

    18．（本小题满分13分）

    解：（1）①只安排2位接线员，则2路及2路以下电话同时打入均能接通，其概率

         

          故所求概率；……………………4分

          ②“损害度” ………………8分

       （2）∵在一天的这一时间内同时电话打入数ξ的数学期望为

          0×0.13+1×0.35+2×0.27+3×0.14+4×0.85+5×0.02+6×0.01=1.79

          ∴一周五个工作日的这一时间电话打入数ξ的数学期望等于5×1.79=8.95.……13分

    19．（1）连结B1D1，过F作B1D1的垂线，垂足为K.

          ∵BB1与两底面ABCD，A1B1C1D1都垂直.

          FK⊥BB1

          ∴FK⊥B1D1             FK⊥平面BDD1B1，

          B1D1∩BB1=B1

          又AE⊥BB1

          又AE⊥BD    AE⊥平面BDD1B1            因此KF∥AE.

          BB1∩BD=B

          ∴∠BFK为异面直线BF与AE所成的角，连结BK，由FK⊥面BDD1B1得FK⊥BK，

          从而△BKF为Rt△.

          在Rt△B1KF和Rt△B1D1A1中，由得：

         

          又BF=.   

          ∴异面直线BF与AE所成的角为arccos.……………………4分

       （2）由于DA⊥平面AA1B由A作BF的垂线AG，垂足为G，连结DG，由三垂线定理

            知BG⊥DG.

          ∴∠AGD即为平面BDF与平面AA1B所成二面角的平面角. 且∠DAG=90°

          在平面AA1B1B中，延长BF与AA1交于点S.

    ∥

    ＝

          ∴A1、F分别是SA、SB的中点.   即SA=2A1A=2=AB.

          ∴Rt△BAS为等腰直角三角形，垂足G点实为斜边SB的中点F，即F、G重合.

          易得AG=AF=SB=，在Rt△BAS中，AD=

          ∴tan∠AGD=

          即平面BDF与平面AA1B1B所成二面角（锐角）的大小为arctan .…………9分

       （3）由（2）知平面AFD是平面BDF与平面AA1B1B所成二面角的平面角所在的平面.

          ∴面AFD⊥面BDF.

          在Rt△ADF中，由A作AH⊥DF于H，则AH即为点A到平面BDF的距离.

          由AH?DF=AD?AF，得

          所以点A到平面BDF的距离为……………………13分

    20．解：（1）∵点都在斜率为6的同一条直线上，

         

          于是数列是等差数列，故……………………3分

          共线，

         

          当n=1时，上式也成立.

          所以………………8分

       （2）把代入上式，

          得

          ，

          ∴当n=4时，取最小值，最小值为………………13分

    21．解：

          ,

          ……………………3分

       （1）的两个实根，

          ∵方程有解，………………7分

       （2）由，

         

          ……………………12分

          法二：

    22．（1）设点T的坐标为，点M的坐标为，则M1的坐标为（0，），

          ，于是点N的坐标为，N1的坐标

          为，所以

          由

          由此得

          由

          即所求的方程表示的曲线C是椭圆. ……………………3分

       （2）点A（5，0）在曲线C即椭圆的外部，当直线l的斜率不存在时，直线l与椭圆C

          无交点，所以直线l斜率存在，并设为k. 直线l的方程为

          由方程组

          依题意

          当时，设交点PQ的中点为，

          则

         

          又

         

          而不可能成立，所以不存在直线l，使得|BP|=|BQ|.…………7分

       （3）由题意有，则有方程组

            由（1）得  （5）

          将（2），（5）代入（3）有

          整理并将（4）代入得，

          易知

          因为B（1，0），S，故，所以

         

          …………12分

     


    同步练习册答案