
题目列表(包括答案和解析)



 ,求△AOB面积的最大值
,求△AOB面积的最大值 的方程;
的方程; 在
在 轴上截距的取值范围;
轴上截距的取值范围; 面积的最大值
面积的最大值椭圆 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合.
(1)求椭圆 和抛物线
和抛物线 的方程;
的方程;
(2)过点F的直线交抛物线 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值.
(3)直线 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.
 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合. 和抛物线
和抛物线 的方程;
的方程; 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值. 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.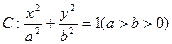
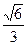
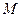
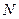
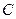
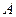
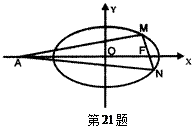 (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;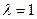 时,
时,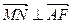 ;
;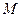 、
、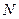 两点在
两点在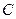 上运动,且
上运动,且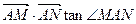 =6
=6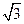 时, 求直线MN的方程
时, 求直线MN的方程
一、选择题
AACCD BBDDD AC
二、填空题
13. 14.6 15.①⑤ 16.
14.6 15.①⑤ 16.
三、解答题
17.解:(Ⅰ)因为 ,
,
由正弦定理,得 , ……3分
, ……3分
整理,得
因为 、
、 、
、 是
是 的三内角,所以
的三内角,所以 ,
,
因此  .
……6分
.
……6分
|