练习册

  • 练习册
  • 试题
    10．解析:-192．本题考查了简单定积分的计算以及求二项式展开式的指定项的基本方法．＝=2 , T= 2x 【查看更多】

     

    题目列表(包括答案和解析)

    （10分）（本题192班必做题，其他班不做）

    已知二次函数f(x)=ax2+bx+c,若f(x)+f(x+1)=2x2－2x+13

    （1）求函数f(x)的解析式；

    （2）画该函数的图象；

    （3）当x∈[t，5]时，求函数f(x)的最大值.

     

    查看答案和解析>>

    （10分）（本题192班不做，其他班必做）

    已知二次函数f（x）满足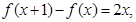且f（0）=1.

    （Ⅰ）求f（x）的解析式;

    （Ⅱ）在区间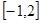上求y= f（x）的值域。

     

    查看答案和解析>>

    已知函数f(x)=
    ax-1
    ax+1
    （a＞0且a≠1），设函数g(x)=f(x-
    1
    2
    )+1    ．
    （1）求证：f（x）是奇函数；
    （2）求g（x）+g（1-x）及g( 0 )+g( 
    1
    4
     )+g( 
    1
    2
     )+g( 
    3
    4
     )+g( 1 )    的值；
    （3）是否存在正整数a，使不等式
    		a
    •g(n)
    g(1-n)
    ＞n2    对一切n∈N*都成立，若存在，求出正整数a的最小值；不存在，说明理由；
    （4）结合本题加以推广：设F（x）是R上的奇函数，请你写出一个函数G（x）的解析式；并根据第（2）小题的结论，猜测函数G（x）满足的一般性结论．

    查看答案和解析>>

    牛奶保鲜时间因储藏时温度的不同而不同，假定保鲜时间与储藏温度是一种指数型关系．若牛奶放在0℃的冰箱中，保鲜时间约是192小时，而在22℃的厨房中则约是42小时，则保鲜时间y（小时）关于储藏温度x（℃）的函数解析式是（　　）

    查看答案和解析>>

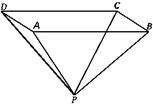    精英家教网用一块钢锭浇铸一个厚度均匀，且全面积为2平方米的正四棱锥形有盖容器（如图），设容器的高为h米，盖子边长为a米．
    （1）求a关于h的函数解析式；
    （2）设容器的容积为V立方米，则当h为何值时，V最大？求出V的最大值．（求解本题时，不计容器的厚度）

    查看答案和解析>>


    同步练习册答案