已知曲线的参数方程是（是参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线:的极坐标方程是=2，正方形ABCD的顶点都在上，且A,B,C,D依逆时针次序排列，点A的极坐标为（2，）.

(Ⅰ)求点A,B,C,D的直角坐标；

 (Ⅱ)设P为上任意一点，求的取值范围.

【命题意图】本题考查了参数方程与极坐标，是容易题型.

【解析】(Ⅰ)由已知可得，，

，，

即A(1，)，B（－，1），C（―1，―），D（，－1），

(Ⅱ)设，令=，

则==，

∵，∴的取值范围是[32,52]

在棱长为的正方体中,是线段的中点,.

(1) 求证:^；

(2) 求证://平面；

(3) 求三棱锥的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中，利用，得到结论，第二问中，先判定为平行四边形，然后，可知结论成立。

第三问中，是边长为的正三角形，其面积为，

因为平面，所以，

所以是直角三角形，其面积为，

同理的面积为， 面积为.  所以三棱锥的表面积为.

解: (1)证明：根据正方体的性质，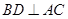

因为，

所以，又，所以，，

所以^.               ………………4分

(2)证明：连接，因为，

所以为平行四边形，因此，

由于是线段的中点，所以，      …………6分

因为面，平面，所以∥平面.   ……………8分

(3)是边长为的正三角形，其面积为，

因为平面，所以，

所以是直角三角形，其面积为，

同理的面积为，              ……………………10分

面积为.          所以三棱锥的表面积为

已知函数，，k为非零实数.

（Ⅰ）设t=k²,若函数f(x),g(x)在区间(0,+∞)上单调性相同，求k的取值范围;

（Ⅱ）是否存在正实数k，都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根，且在[－5,－1]上至多有一个实数根.若存在，请求出所有k的值的集合；若不存在，请说明理由.

【解析】本试题考查了运用导数来研究函数的单调性，并求解参数的取值范围。与此同时还能对于方程解的问题，转化为图像与图像的交点问题来长处理的数学思想的运用。

双曲线的一条渐近线为,由方程组,消去y,得有唯一解,所以△=,

所以,,故选D. w.w.w.k.s.5.u.c.o.m    

答案:D.

【命题立意】:本题考查了双曲线的渐近线的方程和离心率的概念,以及直线与抛物线的位置关系,只有一个公共点,则解方程组有唯一解.本题较好地考查了基本概念基本方法和基本技能.

P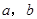（）是平面上的一个点，设事件A表示“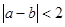”,其中为实常数．

（1）若均为从0，1，2，3，4五个数中任取的一个数，求事件A发生的概率；

（2）若均为从区间[0，5）任取的一个数，求事件A发生的概率．

【解析】本试题考查了几何概型和古典概型结合的一道综合概率计算试题。首先明确区域中的所有基本事件数或者区域表示的面积，然后分别结合概率公式求解得到。