
题目列表(包括答案和解析)
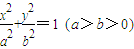 的离心率是
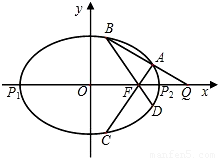
的离心率是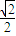 ,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足
,P1、P2是椭圆E的长轴的两个端点(P2位于P1右侧),点F是椭圆E的右焦点.点Q是x轴上位于P2右侧的一点,且满足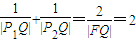 .
.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
| OP |
| OM |
| ON |
| 1 |
| 2 |
已知曲线 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)若过点 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;
(3)以曲线 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与曲线
与曲线 交于点
交于点 与点
与点 ,求
,求 的最小值,并求此时圆
的最小值,并求此时圆 的方程.
的方程.
【解析】第一问利用(1)过点 作直线
作直线 的垂线,垂足为D.
的垂线,垂足为D.
 代入坐标得到
代入坐标得到
第二问当斜率k不存在时,检验得不符合要求;
当直线l的斜率为k时, ;,化简得
;,化简得

第三问点N与点M关于X轴对称,设 ,, 不妨设
,, 不妨设 .
.
由于点M在椭圆C上,所以 .
.
由已知 ,则
,则
 ,
,
由于 ,故当
,故当 时,
时, 取得最小值为
取得最小值为 .
.
计算得, ,故
,故 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 .
.
故圆T的方程为:
(本小题满分12分)
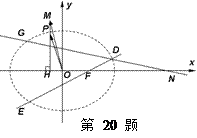
如图,点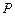 是椭圆
是椭圆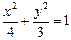 上一动点,点
上一动点,点 是点
是点 在
在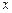 轴上的射影,坐标平面
轴上的射影,坐标平面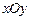 内动点
内动点 满足:
满足: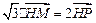 (
( 为坐标原点),设动点
为坐标原点),设动点 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程并画出草图;
的方程并画出草图;
(Ⅱ)过右焦点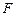 的直线
的直线 交曲线
交曲线 于
于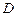 ,
,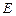 两点,且
两点,且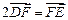 ,点
,点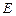 关于
关于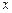 轴的对称点为
轴的对称点为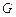 ,求直线
,求直线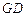 的方程.
的方程.
(本小题满分12分)
如图,点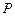 是椭圆
是椭圆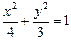 上一动点,点
上一动点,点 是点
是点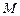 在
在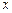 轴上的射影,坐标平面
轴上的射影,坐标平面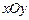 内动点
内动点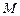 满足:
满足: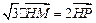 (
( 为坐标原点),设动点
为坐标原点),设动点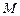 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程并画出草图;
的方程并画出草图;
(Ⅱ)过右焦点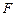 的直线
的直线 交曲线
交曲线 于
于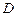 ,
,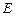 两点,且
两点,且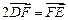 ,点
,点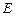 关于
关于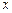 轴的对称点为
轴的对称点为 ,求直线
,求直线 的方程.
的方程.
一、选择题
AACCD BBDDD AC
二、填空题
13. 14.T13 15.①⑤ 16.
14.T13 15.①⑤ 16.
三、解答题
17.解:(Ⅰ)因为 ,
,
由正弦定理,得 ,
……3分
,
……3分
整理,得
因为 、
、 、
、 是
是 的三内角,所以
的三内角,所以 ,
,
因此  .
……6分
.
……6分
(Ⅱ) ,即
,即 ,
……8分
,
……8分
由余弦定理,得 ,所以
,所以 , ……10分
, ……10分
解方程组 ,得
,得 .
……12分
.
……12分
18.(本题满分12分)
解法一:记 与
与 的比赛为
的比赛为 ,
,
(Ⅰ)齐王与田忌赛马,有如下六种情况:
 ,
, ,
,
 ,
,  ,
,
 ,
,  . ………………………3分
. ………………………3分
其中田忌获胜的只有一种 ,所以田忌获胜的概率为
,所以田忌获胜的概率为 .
.
…………………………………………………………………………………………6分
(Ⅱ)已知齐王第一场必出上等马 ,若田忌第一场出上等马
,若田忌第一场出上等马 或中等马
或中等马 ,则剩下两场中至少输掉一场,这时田忌必败.
,则剩下两场中至少输掉一场,这时田忌必败.
为了使自己获胜的概率最大,田忌第一场应出下等马 ,后两场有两种情形:
,后两场有两种情形:
①若齐王第二场派出中等马 ,可能对阵情形是
,可能对阵情形是 、
、
或者 、
、 ,所以田忌获胜的概率为
,所以田忌获胜的概率为 ; ………………………9分
; ………………………9分
②若齐王第二场派出下等马 ,可能对阵情形是
,可能对阵情形是 、
、
或者 、
、 ,所以田忌获胜的概率为
,所以田忌获胜的概率为 ,
,
所以田忌按 或者
或者 的顺序出马,才能使自己获胜的概率达到最大值
的顺序出马,才能使自己获胜的概率达到最大值 .
.
………………………………………………………………………………………12分
解法二:各种对阵情况列成下列表格:



1



2



3



4



5



6



………………………3分
(Ⅰ)其中田忌获胜的只有第五种这一种情形,所以田忌获胜的概率为 .……6分
.……6分
(Ⅱ)为了使自己获胜的概率最大,田忌第一场应出下等马 ,即只能是第五、第六两种情形. …………………………………………………9分
,即只能是第五、第六两种情形. …………………………………………………9分
其中田忌获胜的只有第五种这一种情形,所以田忌按 或者
或者 的顺序出马,才能使自己获胜的概率达到最大值
的顺序出马,才能使自己获胜的概率达到最大值 .………………………12分
.………………………12分
19.(本题满分12分)
 解证: (Ⅰ) 连结
解证: (Ⅰ) 连结 连结
连结 ,
,
∵四边形 是矩形
是矩形
∴ 为
为 中点
中点
又 为
为 中点,从而
中点,从而 ∥
∥ ------------3分
------------3分
∵ 平面
平面 ,
, 平面
平面
∴ ∥平面
∥平面 。-----------------------5分
。-----------------------5分
(Ⅱ)(方法1)
三角形 的面积
的面积 -------------------8分
-------------------8分
 到平面
到平面 的距离为
的距离为 的高
的高
∴ ---------------------------------11分
---------------------------------11分
因此,三棱锥 的体积为
的体积为 。------------------------------------12分
。------------------------------------12分
(方法2)

 ,
,
 ,
,
∴ 为等腰
为等腰 ,取底边
,取底边 的中点
的中点 ,
,
则 ,
,
∴ 的面积
的面积 -----------8分
-----------8分
∵ ,∴点
,∴点 到平面
到平面 的距离等于
的距离等于 到平面
到平面
 的距离,
的距离,
由于 ,
, ,
,
∴  ,
,
过 作
作 于
于 ,则
,则 就是
就是 到平面
到平面 的距离,
的距离,
又 ,----------11分
,----------11分
 ---------------------12分
---------------------12分
(方法3)
 到平面
到平面 的距离为
的距离为 的高
的高
∴四棱锥 的体积
的体积 ------------------------9分
------------------------9分
三棱锥 的体积
的体积
∴ ---------------------------------------------11分
---------------------------------------------11分
因此,三棱锥 的体积为
的体积为 。-------------------------------------12分
。-------------------------------------12分
20.(Ⅰ)依题意知,
∵ ,
,
∴ .
.
∴所求椭圆 的方程为
的方程为 .
……4分
.
……4分
(Ⅱ)设点
 关于直线
关于直线 的对称点为
的对称点为 ,
,
∴  ……6分
……6分
解得: ,
, .
……8分
.
……8分
∴ .
……10分
.
……10分
∵ 点
 在椭圆
在椭圆 :
: 上,
上,
∴ , 则
, 则 .
.
∴ 的取值范围为
的取值范围为 .
……12分
.
……12分
21.解:(Ⅰ)由 知,
知, 定义域为
定义域为 ,
,
 . ……………………3分
. ……………………3分
当 时,
时, ,
………………4分
,
………………4分
当 时,
时, .
………………5分
.
………………5分
所以 的单调增区间是
的单调增区间是 ,
,
 的单调减区间是
的单调减区间是 .
…………………… ………………6分
.
…………………… ………………6分
(Ⅱ)由(Ⅰ)知, 在
在 上单调递增,
上单调递增,
在 上单调递减,在
上单调递减,在 上单调递增,且当
上单调递增,且当 或
或 时,
时,
 , 所以
, 所以 的极大值为
的极大值为 ,
,
极小值为 . ………………………8分
. ………………………8分
又因为 ,
,
 , ………10分
, ………10分
所以在 的三个单调区间
的三个单调区间 上,
上,
直线 与
与 的图象各有一个交点,
的图象各有一个交点,
当且仅当 , 因此,
, 因此,
 的取值范围为
的取值范围为 . ………………12分
. ………………12分
22.解:(Ⅰ)当 时,
时, ……………………………3分
……………………………3分
∴ =
=
=
=
= …………………………………7分
…………………………………7分
(Ⅱ) 

 +
+
 +
+

=
= ……………13分
……………13分
当且仅当 ,即
,即 时,
时, 最小.……………………14分
最小.……………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com