
题目列表(包括答案和解析)
设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() .”
.”
(1)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(2)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意
的定义域为D,则对于任意![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(3)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中任意的
定义域中任意的![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() .
.
设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]()
![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() .”
.”
(I)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意
的定义域为D,则对于任意
[m,n]![]() D,都存在
D,都存在![]()
![]() [m,n],使得等式
[m,n],使得等式![]() 成立”,
成立”,
试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(III)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中任意的
定义域中任意的![]() .
.
设M是由满足下列条件的函数 构成的集合:①方程,
构成的集合:①方程, 有实数根②函数
有实数根②函数 的导数
的导数 满足
满足 .
.
(I)
若函数 为集合M中的任意一个元素,证明:方程
为集合M中的任意一个元素,证明:方程 只有一个实数根;
只有一个实数根;
(II)
判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(III) 设函数 为集合M中的任意一个元素,对于定义域中任意
为集合M中的任意一个元素,对于定义域中任意 ,当
,当 ,且
,且 时,证明:
时,证明: .
.
设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程 有实数
有实数
根;②函数 ”[来源:学+科+网Z+X+X+K]
”[来源:学+科+网Z+X+X+K]
(I)判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(II)集合M中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为D,则对于任意
的定义域为D,则对于任意
 成立。试用这一性
成立。试用这一性
质证明:方程 只有一个实数根;
只有一个实数根;
(III)对于M中的函数 的实数根,求证:对于
的实数根,求证:对于 定义
定义
域中任意的 当
当 且
且
 构成的集合:①方程,
构成的集合:①方程, 有实数根②函数
有实数根②函数 的导数
的导数 满足
满足 .
. 为集合M中的任意一个元素,证明:方程
为集合M中的任意一个元素,证明:方程 只有一个实数根;
只有一个实数根; 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;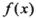 为集合M中的任意一个元素,对于定义域中任意
为集合M中的任意一个元素,对于定义域中任意 ,当
,当 ,且
,且 时,证明:
时,证明: .
.一、选择题:
1.C 2.D3.A4.C 5.C6.A7.B 8.D9.B10.D11.B 12.B
二、填空题:
13、.files/image304.gif) 14、
14、.files/image306.gif) 15、1
16、一 17、4
18、56 19、
15、1
16、一 17、4
18、56 19、.files/image308.gif) 20、
20、.files/image310.gif) 21、
21、.files/image312.gif) 22、4/9 23、② 24、
22、4/9 23、② 24、.files/image314.gif) 25、
25、.files/image316.gif) 26、①
26、①
三、解答题:
16、解: (Ⅰ).files/image318.gif)
.files/image320.gif) ,
,
∴.files/image322.gif) ,
,
解得.files/image324.gif) .
.
(Ⅱ)由.files/image212.gif) ,得:
,得:.files/image326.gif) ,
,
∴.files/image328.gif)
∴.files/image330.gif)
17、解:(1).files/image332.gif)
则.files/image217.gif) 的最小正周期
的最小正周期.files/image334.gif) ,
,
且当.files/image336.gif) 时
时.files/image217.gif) 单调递增.
单调递增.
即.files/image338.gif) 为
为.files/image217.gif) 的单调递增区间(写成开区间不扣分).………6分
的单调递增区间(写成开区间不扣分).………6分
(2)当.files/image219.gif) 时
时.files/image340.gif) ,当
,当.files/image342.gif) ,即
,即.files/image344.gif) 时
时.files/image346.gif) .
.
所以.files/image348.gif) .
.
.files/image350.gif) 为
为.files/image217.gif) 的对称轴.
的对称轴.
18、解:(Ⅰ)解法一:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,记“有放回摸球两次,两球恰好颜色不同”为事件.files/image352.gif) ,
,
∵“两球恰好颜色不同”共.files/image354.gif) 种可能,
种可能,
∴.files/image356.gif) .
.
解法二:“有放回摸取”可看作独立重复实验,
∵每次摸出一球得白球的概率为.files/image358.gif) .
.
∴“有放回摸两次,颜色不同”的概率为.files/image360.gif) .
.
(Ⅱ)设摸得白球的个数为.files/image362.gif) ,依题意得:
,依题意得:
.files/image364.gif) ,
,
.files/image366.gif) ,
,
.files/image368.gif) .
.
∴.files/image370.gif) ,
,
.files/image372.gif) .
.
19、(Ⅰ)证明: 连结.files/image374.gif) ,
,.files/image376.gif) 与
与.files/image374.gif) 交于点
交于点.files/image378.gif) ,连结
,连结.files/image380.gif) .
.
.files/image389.gif)
.files/image318.gif)
.files/image235.gif) 是菱形, ∴
是菱形, ∴.files/image378.gif) 是
是.files/image374.gif) 的中点.
的中点.
.files/image318.gif) 点
点.files/image241.gif) 为
为.files/image243.gif) 的中点, ∴
的中点, ∴.files/image393.gif) .
.
.files/image395.gif) 平面
平面.files/image397.gif) 平面
平面.files/image247.gif) , ∴
, ∴.files/image245.gif) 平面
平面.files/image247.gif) .
.
(Ⅱ)解法一:
.files/image318.gif)
.files/image237.gif) 平面
平面.files/image235.gif) ,
,.files/image401.gif) 平面
平面.files/image235.gif) ,∴
,∴ .files/image403.gif) .
.
.files/image405.gif) ,∴
,∴.files/image407.gif) .
.
.files/image318.gif)
.files/image235.gif) 是菱形, ∴
是菱形, ∴.files/image410.gif) .
.
.files/image412.gif) ,
,
∴.files/image414.gif) 平面
平面.files/image416.gif) .
.
作.files/image418.gif) ,垂足为
,垂足为.files/image420.gif) ,连接
,连接.files/image422.gif) ,则
,则.files/image424.gif) ,
,
所以.files/image426.gif) 为二面角
为二面角.files/image427.gif) 的平面角.
的平面角.
.files/image318.gif)
.files/image239.gif) ,∴
,∴.files/image430.gif) ,
,.files/image432.gif) .
.
在Rt△.files/image434.gif) 中,
中,.files/image436.gif) =
=.files/image438.gif)
.files/image440.gif) ,
,
∴.files/image442.gif) .
.
∴二面角.files/image249.gif) 的正切值是
的正切值是.files/image444.gif) .
.
解法二:如图,以点.files/image352.gif) 为坐标原点,线段
为坐标原点,线段.files/image447.gif) 的垂直平分线所在直线为
的垂直平分线所在直线为.files/image449.gif) 轴,
轴,.files/image451.gif) 所在直线为
所在直线为.files/image453.gif) 轴,
轴,.files/image455.gif) 所在直线为
所在直线为.files/image457.gif) 轴,建立空间直角坐标系,令
轴,建立空间直角坐标系,令.files/image459.gif) ,
,
则.files/image461.gif) ,
,.files/image463.gif) ,
,.files/image465.gif) .
.
.files/image469.gif) ∴
∴.files/image471.gif) .
.
设平面.files/image473.gif) 的一个法向量为
的一个法向量为.files/image475.gif)
.files/image477.gif) ,
,
由.files/image475.gif)
.files/image480.gif)
.files/image475.gif)
.files/image483.gif) ,得
,得.files/image485.gif) ,
,
令.files/image487.gif) ,则
,则.files/image489.gif) ,∴
,∴.files/image491.gif) .
.
.files/image318.gif)
.files/image237.gif) 平面
平面.files/image235.gif) ,
,.files/image401.gif) 平面
平面.files/image235.gif) ,
,
∴.files/image403.gif) .
.
.files/image405.gif) ,∴
,∴.files/image407.gif) .
.
.files/image318.gif)
.files/image235.gif) 是菱形,∴
是菱形,∴.files/image410.gif) .
.
.files/image412.gif) ,∴
,∴.files/image414.gif) 平面
平面.files/image247.gif) .
.
∴.files/image499.gif) 是平面
是平面.files/image247.gif) 的一个法向量,
的一个法向量,.files/image502.gif)
.files/image504.gif) .
.
∴.files/image506.gif) ,
,
∴.files/image508.gif) ,
,
∴.files/image510.gif) .
.
∴二面角.files/image249.gif) 的正切值是
的正切值是.files/image444.gif) .
.
20、解:圆.files/image265.gif) 的方程为
的方程为.files/image513.gif) ,则其直径长
,则其直径长.files/image515.gif) ,圆心为
,圆心为.files/image517.gif) ,设
,设.files/image267.gif) 的方程为
的方程为.files/image520.gif) ,即
,即.files/image522.gif) ,代入抛物线方程得:
,代入抛物线方程得:.files/image524.gif) ,设
,设.files/image526.gif) ,
,
.files/image527.gif) 有
有.files/image529.gif) ,
,
则.files/image531.gif) .
.
故.files/image533.gif) …6分
…6分
.files/image535.gif) ,
,
因此.files/image537.gif) .
.
据等差,.files/image539.gif) ,
,
所以.files/image541.gif) ,即
,即.files/image543.gif) ,
,.files/image545.gif) ,分
,分
即:.files/image267.gif) 方程为
方程为.files/image548.gif) 或
或.files/image550.gif) .
.
21、解:(1)因为.files/image552.gif) ,
,
所以.files/image554.gif) ,满足条件
,满足条件.files/image556.gif) .
.
又因为当.files/image558.gif) 时,
时,.files/image560.gif) ,所以方程
,所以方程.files/image291.gif) 有实数根
有实数根.files/image563.gif) .
.
所以函数.files/image281.gif) 是集合M中的元素.
是集合M中的元素.
(2)假设方程.files/image291.gif) 存在两个实数根
存在两个实数根.files/image566.gif) ),
),
则.files/image568.gif) ,
,
不妨设.files/image570.gif) ,根据题意存在数
,根据题意存在数.files/image572.gif)
使得等式.files/image574.gif) 成立,
成立,
因为.files/image576.gif) ,所以
,所以.files/image578.gif) ,与已知
,与已知.files/image279.gif) 矛盾,
矛盾,
所以方程.files/image291.gif) 只有一个实数根;
只有一个实数根;
(3)不妨设.files/image582.gif) ,因为
,因为.files/image584.gif) 所以
所以.files/image217.gif) 为增函数,所以
为增函数,所以.files/image587.gif) ,
,
又因为.files/image589.gif) ,所以函数
,所以函数.files/image591.gif) 为减函数,
为减函数,
所以.files/image593.gif) ,
,
所以.files/image595.gif) ,即
,即.files/image597.gif) ,
,
所以.files/image599.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com