（本小题满分14分）

如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN，要求B在AM上，D在AN上，且对角线MN过C点，|AB|=3米，|AD|=2米.

   （Ⅰ）要使矩形AMPN的面积大于32平方米，则AN的长应在什么范围内？

   （Ⅱ）若AN的长度不小于6米，则当AM、AN的长度是多少时，矩形AMPN的面积最小？并求出最小面积.

 

 

 

 

 

 

 

 

（本小题满分14分）如图所示，某市政府决定在以政府大楼O为中心、正北方向

和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地，并考

虑与周边环境协调，设计要求该图书馆底面矩形的四个顶点都要在边界上，图书馆的正

面要朝市政府大楼.设扇形的半径OM＝R 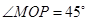，，OB与OM之间的夹角为.

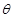（1）将图书馆底面矩形ABCD的面积S表示成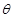的函数.

（2）若 R＝45 m，求当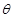为何值时，矩形ABCD的面积S有最大值？

其最大值是多少？

 

 

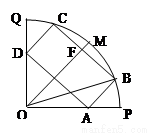
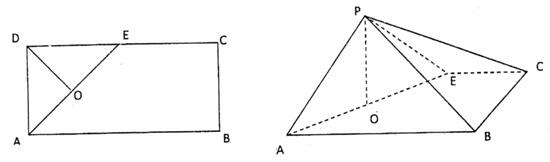
（本小题满分14分）

如图所示，在矩形中，的中点，O为AE的中点，以AE为折痕将△ADE向上折起，使D到P点位置，且.

（Ⅰ）求证：

（Ⅱ）求二面角E-AP-B的余弦值.

 

（本小题满分14分）

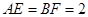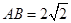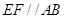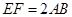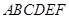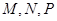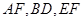如图1，在等腰梯形CDEF中，CB、DA是梯形的高，，,现将梯形沿CB、DA折起，使且，得一简单组合体如图2示，已知分别为的中点．

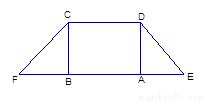
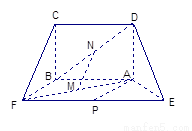
图1                                图2

（1）求证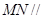：平面；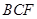

（2）求证：；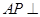

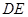（3）当多长时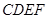，平面与平面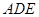所成的锐二面角为？

 

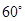（本小题满分14分）

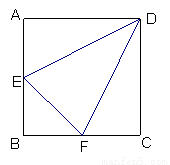
如图①边长为1的正方形ABCD中，点E、F分别

为AB、BC的中点，将△BEF剪去，将

△AED、△DCF分别沿DE、DF折起，使A、

C两点重合于点P得一个三棱锥如图②示.              

（1）求证：;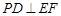

（2）求三棱锥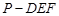的体积；                

（3）求DE与平面PDF所成角的正弦值.