1,3,5
2.B 利用数形结合求解,令数学试题(文科).files/image117.gif) 的交点个数.
的交点个数.
3.C 解析:取满足数学试题(文科).files/image119.gif) 可得答案C.
可得答案C.
4.B 解析:取答案各区间的特点值数学试题(文科).files/image121.gif) 代入检验即可.
代入检验即可.
5.D 解析:B、C的函数周期为2数学试题(文科).files/image028.gif) ,不合题意,A的函数在区间
,不合题意,A的函数在区间数学试题(文科).files/image024.gif) 上为增函数,不合题意
上为增函数,不合题意
6.D 解析:由a1=2知答案A不正确,再由a1+a2=S2=4a2数学试题(文科).files/image125.gif) 可得答案B、C不正确
可得答案B、C不正确
7.A 解析:数学试题(文科).files/image127.gif)
数学试题(文科).files/image129.gif) ,故选A.
,故选A.
8.A 解析:数学试题(文科).files/image131.gif)
=2k+数学试题(文科).files/image133.gif) ,故选A.
,故选A.
9.D 解析:数学试题(文科).files/image135.gif) 满足
满足数学试题(文科).files/image137.gif)
数学试题(文科).files/image139.gif) ,故a的取值范围是
,故a的取值范围是数学试题(文科).files/image072.gif) ,故选D.
,故选D.
10.B 解析:①、②正确,③、④错误,因为③、④中对于虚数的情况没有大小关系,故选B.
二、填空题
11.答案:1-i 解析:数学试题(文科).files/image142.gif)
12.答案:81 解析:数学试题(文科).files/image144.gif)
13.答案:数学试题(文科).files/image146.gif) 解析:∵
解析:∵数学试题(文科).files/image148.gif) ,当且仅当
,当且仅当数学试题(文科).files/image150.gif) 时取等号.
时取等号.
14.答案:18 解析:每行的数字取值从(n-1)2+1到n2,而172<300<182,故300在第18行.
三、解答题:
15.解:∵数学试题(文科).files/image152.gif) ,
,
∴命题P为真时数学试题(文科).files/image154.gif)
命题P为假时数学试题(文科).files/image156.gif)
命题Q为真时,数学试题(文科).files/image158.gif)
命题Q为假时 数学试题(文科).files/image160.gif)
由“P\/Q”为真且“P/\Q”为假,知P、Q有且只有一个正确.
情形(1):P正确,且Q不正确数学试题(文科).files/image162.gif)
情形(2):P不正确,且Q正确数学试题(文科).files/image164.gif)
综上,a取值范围是数学试题(文科).files/image166.gif)
另解:依题意,命题P为真时,0<a<1
曲线数学试题(文科).files/image100.gif) 轴交于两点等价于
轴交于两点等价于数学试题(文科).files/image169.gif) ,
,
得
数学试题(文科).files/image171.gif) 故命题Q为真时,
故命题Q为真时,数学试题(文科).files/image171.gif)
由“P\/Q”为真且“P/\Q”为假,知P、Q有且只有一个正确.
等价于P、Q为真时在数轴表示图形中有且只有一个阴影的部分.
数学试题(文科).files/image174.jpg)
(注:如果答案中数学试题(文科).files/image176.gif) 端点取了开区间,扣2分) 端点取了开区间,扣2分) 16.解:设此工厂应分别生产甲、乙两种产品x吨、y吨. 获得利润z万元
数学试题(文科).files/image178.jpg)
作出可行域如右图 利润目标函数z=6x+12y 由几何意义知当直线l:z=6x+12y,经过可行域上的点M时,z=6x+12y取最大值. 解方程组 数学试题(文科).files/image182.gif) ,得M(20,24) ,得M(20,24) 答:生产甲种产品20t,乙种产品24t,才能使此工厂获得最大利润 17.解:(Ⅰ)∵A+B+C=180° 由数学试题(文科).files/image184.gif) ∴数学试题(文科).files/image186.gif) 整理,得数学试题(文科).files/image188.gif) 解得:
解得:数学试题(文科).files/image190.gif) ∵数学试题(文科).files/image192.gif) ∴C=60° ∴C=60° (Ⅱ)由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-2ab ∴数学试题(文科).files/image194.gif) =25-3ab =25-3ab数学试题(文科).files/image196.gif) ∴数学试题(文科).files/image198.gif) 18.解:(1)由条件得:数学试题(文科).files/image200.gif) (2)数学试题(文科).files/image202.gif) ① ① ∴6Tn=6+6×62+11×63+…+(5n-4)6n ② ①-②:数学试题(文科).files/image204.gif) 数学试题(文科).files/image206.gif)
∴数学试题(文科).files/image208.gif) 19.解:设AM的长为x米(x>3)
数学试题(文科).files/image210.jpg)
∴数学试题(文科).files/image216.gif) …………3分 …………3分 (Ⅰ)由SAMPN>32得数学试题(文科).files/image218.gif) , , ∵数学试题(文科).files/image220.gif) 即AM长的取值范围是(3,4)数学试题(文科).files/image222.gif) (Ⅱ)令数学试题(文科).files/image224.gif) ∴当数学试题(文科).files/image226.gif) 上单调递增,x<6, 上单调递增,x<6,数学试题(文科).files/image228.gif) ,函数在(3,6)上单调递减 ,函数在(3,6)上单调递减 ∴当x=6时,数学试题(文科).files/image230.gif) 取得最小值即SAMPN取得最小值24(平方米) 取得最小值即SAMPN取得最小值24(平方米) 此时|AM|=6米,|AN|=4米 答:当AM、AN的长度分别是6米、4米时,矩形AMPN的面积最小,最小面积是24平方米. 另解:以AM、AN分别为x、y轴建立直角坐标系, 设数学试题(文科).files/image232.gif) 由C在直线MN上得 数学试题(文科).files/image234.gif) ∴数学试题(文科).files/image236.gif) 数学试题(文科).files/image238.gif)
∴AM的长取值范围是(3,4)数学试题(文科).files/image222.gif) (Ⅱ)∵数学试题(文科).files/image240.gif) 时等号成立. 时等号成立. ∴|AM|=6米,|AN|=4米时,SAMPN达到最小值24 答:当AM、AN的长度分别是6米、4米时,矩形AMPN的面积最小,最小面积是24平方米. 20.解:(1)设x<0,则-x>0 ∵数学试题(文科).files/image115.gif) 为偶函数, ∴ 为偶函数, ∴数学试题(文科).files/image242.gif) (2)∵数学试题(文科).files/image115.gif) 为偶函数,∴ 为偶函数,∴数学试题(文科).files/image115.gif) =0的根关于0对称. =0的根关于0对称. 由数学试题(文科).files/image115.gif) =0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根. =0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根. 且两个正根和二个负根互为相反数 ∴原命题数学试题(文科).files/image244.gif) 图像与x轴恰有两个不同的交点 图像与x轴恰有两个不同的交点 下面研究x>0时的情况 ∵数学试题(文科).files/image246.gif) 即 数学试题(文科).files/image248.gif) 为单调增函数,故 为单调增函数,故数学试题(文科).files/image250.gif) 不可能有两实根 不可能有两实根 ∴a>0 令数学试题(文科).files/image252.gif) 当数学试题(文科).files/image254.gif) 递减, 递减, ∴数学试题(文科).files/image256.gif) 处取到极大值 处取到极大值数学试题(文科).files/image258.gif) 又当数学试题(文科).files/image260.gif) 要使数学试题(文科).files/image262.gif) 轴有两个交点当且仅当 轴有两个交点当且仅当数学试题(文科).files/image258.gif) >0 >0 解得数学试题(文科).files/image265.gif) ,故实数a的取值范围(0, ,故实数a的取值范围(0,数学试题(文科).files/image267.gif) ) ) 方法二: (2)∵数学试题(文科).files/image115.gif) 为偶函数, ∴ 为偶函数, ∴数学试题(文科).files/image115.gif) =0的根关于0对称. =0的根关于0对称. 由数学试题(文科).files/image115.gif) =0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根. =0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根. 且两个正根和二个负根互为相反数 ∴原命题数学试题(文科).files/image244.gif) 图像与x轴恰有两个不同的交点 图像与x轴恰有两个不同的交点 下面研究x>0时的情况 数学试题(文科).files/image269.gif) 与直线 与直线数学试题(文科).files/image271.gif) 交点的个数. 交点的个数.
∴当数学试题(文科).files/image273.gif) 时, 时,数学试题(文科).files/image275.gif) 递增与直线y=ax下降或是x国, 递增与直线y=ax下降或是x国, 故交点的个数为1,不合题意 ∴a>0
数学试题(文科).files/image277.jpg)
设切点数学试题(文科).files/image280.gif) ∴切线方为 数学试题(文科).files/image282.gif) 由切线与y=ax重合知数学试题(文科).files/image284.gif) 故实数a的取值范围为(0,数学试题(文科).files/image267.gif) ) )
| | | | | | | |

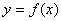 是定义在R上的奇函数,当
是定义在R上的奇函数,当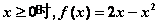 ,
,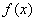 的解析式;
的解析式;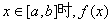 的值域为
的值域为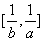 ?若存在,求出所有的a,b的值;若不存在说明理由.
?若存在,求出所有的a,b的值;若不存在说明理由. 的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
的图象如图所示,直线BD∥AC,且直线BD与函数图象切于点B,交于点D,直线AC与函数图象切于点C,交于点A.
 的最大值 ;
的最大值 ; 的单调递减区间;
的单调递减区间; ,
, ,
, ,
,
 ;
; (a
> 0,且a ≠ 1)的解集是{ x | x < 0 };
(a
> 0,且a ≠ 1)的解集是{ x | x < 0 }; 的定义域为R.如果
的定义域为R.如果 为真命题,
为真命题, 为假命题,
为假命题,