
题目列表(包括答案和解析)
(1)求实数t的取值范围;
(2)是否存在实数t,使得线段AB(包括两端点)与直线x=1相交?若存在,求出t的取值范围;若不存在,请说明理由.
(文)已知函数f(x)=mx3-x的图像上,以N(1,n)为切点的切线的倾斜角为![]() .
.
(1)求m,n的值;
(2)是否存在最小的正整数k,使得不等式f(x)≤k-1991对于x∈[-1,3]恒成?如果存在,请求出最小的正整数k;如果不存在,请说明理由。
(3)求证:|f(sinx)+f(cosx)|≤2f(t+![]() )(x∈R,t>0).
)(x∈R,t>0).
(理)已知电流I与时间t的关系式为:I=Asin(ωt+φ)(ω>0,|φ|<π/2),如图是其在一个周期内的图象

(1)求I的解析式
(2)若t在任意一段1/150秒的时间内,电流I都能取得最大、最小值,那么ω的最小正整数是多少?
| f(x1)-f(x2) |
| x1-x2 |
| 5 |
| 2 |
| n+1 |
| n |
| n-1 |
| n3 |
设![]() ,等差数列
,等差数列![]() 中
中![]() ,
,![]() ,记
,记![]() =
=![]() ,令
,令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 的通项公式和
的通项公式和![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)是否存在正整数![]() ,且
,且![]() ,使得
,使得![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
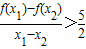 ;
;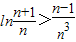 恒成立.
恒成立.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com