
题目列表(包括答案和解析)
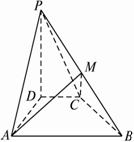
(1)若PB中点为M,求证平面AMC⊥平面PBC;
(2)求异面直线PA与BC所成的角.
(1)建立适当的坐标系,并写出点B、P的坐标;
(2)求异面直线PA与BC所成的角;
(3)若PB的中点为M,求证:平面AMC⊥平面PBC.
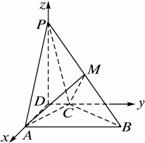
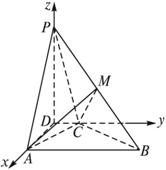
(1)建立适当的坐标系,并写出点B、P的坐标;
(2)求异面直线PA与BC所成的角;
(3)若PB的中点为M,求证:平面AMC⊥平面PBC.
(1)建立适当的坐标系,并写出点B、P的坐标;
(2)求异面直线PA与BC所成的角;
(3)若PB的中点为M,求证:平面AMC⊥平面PBC.

如图,在四棱锥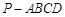 中,底面
中,底面 为矩形,
为矩形,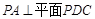 .
.
(1)求证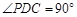 ,并指出异面直线PA与CD所成角的大小;
,并指出异面直线PA与CD所成角的大小;
(2)在棱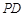 上是否存在一点
上是否存在一点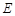 ,使得
,使得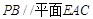 ?如果存在,求出此时三棱锥
?如果存在,求出此时三棱锥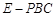 与四棱锥
与四棱锥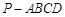 的体积比;如果不存在,请说明理由.
的体积比;如果不存在,请说明理由.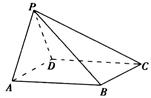
一、选择题
1.D 2.A 3.A 4.C 5.D 6.D 7.B 8.A
二、填空题
9.数学试题(理科).files/image122.gif) 10.
10.数学试题(理科).files/image124.gif) 11.40;
11.40;数学试题(理科).files/image126.gif) 12.7 13.3 14.①②③④
12.7 13.3 14.①②③④
三、解答题
15.解:(1)设数列数学试题(理科).files/image128.gif)
由题意得:数学试题(理科).files/image130.gif)
解得:数学试题(理科).files/image132.gif)
(2)依题数学试题(理科).files/image134.gif) ,
,
数学试题(理科).files/image136.gif) 为首项为2,公比为4的等比数列
为首项为2,公比为4的等比数列
(2)由数学试题(理科).files/image138.gif)
数学试题(理科).files/image140.gif)
16.解:(1)数学试题(理科).files/image142.gif) ,
,
数学试题(理科).files/image144.gif)
(2)由数学试题(理科).files/image146.gif)
数学试题(理科).files/image148.gif)
17.解法1:
设轮船的速度为x千米/小时(x>0),
则航行数学试题(理科).files/image150.gif) 小时。
小时。
依题意,设与速度有关的每小时燃料费用为数学试题(理科).files/image152.gif) ,
,
数学试题(理科).files/image154.gif)
答:轮船的速度应定为每小时20公里,行驶
解法2:
设轮船的速度为x千米/小时(x>0),
则航行数学试题(理科).files/image150.gif) 小时,
小时,
依题意,设与速度有关的每小时燃料费用为数学试题(理科).files/image152.gif)
数学试题(理科).files/image157.gif)
数学试题(理科).files/image159.gif) 元,
元,
且当数学试题(理科).files/image161.gif) 时等号成立。
时等号成立。
答:轮船的速度应定为每小时20公里,行驶
18.解:(1)数学试题(理科).files/image163.gif) ,半径为1依题设直线
,半径为1依题设直线数学试题(理科).files/image165.gif) ,
,
由圆C与l相切得:数学试题(理科).files/image167.gif)
(2)设线段AB中点为数学试题(理科).files/image169.gif)
代入数学试题(理科).files/image171.gif) 即为所求的轨迹方程。
即为所求的轨迹方程。
(3)数学试题(理科).files/image173.gif)
数学试题(理科).files/image175.gif)
|