
题目列表(包括答案和解析)
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
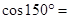 ( )
( )
A.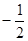 B.
B. C.
C.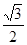 D.
D.
 =(
)
=(
)
A. B.
B. C.
C. D.
D.
一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分数.
一.选择题:BBDC DDAD
1.将各选项代入检验易得答案选B.
2..files/image259.gif) ,图中阴影部分表示的集合为
,图中阴影部分表示的集合为.files/image261.gif) ,选B.
,选B.
3.由函数以.files/image042.gif) 为周期,可排除A、B,由函数在
为周期,可排除A、B,由函数在.files/image040.gif) 为增函数,可排除C,故选D。
为增函数,可排除C,故选D。
4..files/image263.gif) 或
或.files/image265.gif)
.files/image267.gif) 或
或.files/image060.gif) ,故选C。
,故选C。
.files/image270.gif) 5.该程序的功能是求和
5.该程序的功能是求和.files/image272.gif) ,因输出结果
,因输出结果.files/image274.gif) ,故选D.
,故选D.
6.由已知得.files/image276.gif) 即
即.files/image278.gif)
.files/image280.gif) ,故选D.
,故选D.
7.如图:易得答案选A.
8.若.files/image123.gif) 成立,依题意则应有当
成立,依题意则应有当.files/image282.gif) 时,均有
时,均有.files/image127.gif) 成立,故A不成立,
成立,故A不成立,
若.files/image129.gif) 成立,依题意则应有当
成立,依题意则应有当.files/image284.gif) 时,均有
时,均有.files/image127.gif) 成立,故B不成立,
成立,故B不成立,
因命题“当.files/image117.gif) 成立时,总可推 出
成立时,总可推 出.files/image119.gif)
.files/image121.gif) 成立”.
成立”..files/image286.gif) “当
“当.files/image288.gif)
.files/image121.gif) 成立时,总可推出
成立时,总可推出.files/image290.gif) 成立”.因而若
成立”.因而若.files/image134.gif) 成立,则当
成立,则当.files/image292.gif) 时,均有
时,均有.files/image138.gif) 成立 ,故C也不成立。对于D,事实上
成立 ,故C也不成立。对于D,事实上.files/image140.gif)
.files/image294.gif) ,依题意知当
,依题意知当.files/image142.gif) 时,均有
时,均有.files/image144.gif) 成立,故D成立。
成立,故D成立。
二.填空题:9.800、20%;10. .files/image296.gif) ;11. 3;12. ①③④⑤;13.
;11. 3;12. ①③④⑤;13. .files/image298.gif) ;14. 2或8;15.
;14. 2或8;15. .files/image300.gif)
9. 由率分布直方图知,及格率=.files/image302.gif) =80%,
=80%,
及格人数=80%×1000=800,优秀率=.files/image304.gif) %.
%.
10.解一:任取3个球有C.files/image306.gif) 种结果,编号之和为奇数的结果数为C
种结果,编号之和为奇数的结果数为C.files/image308.gif) C
C.files/image310.gif) + C
+ C.files/image312.gif) =60,故所求概率为
=60,故所求概率为.files/image314.gif) .
.
解二:十个球的编号中,恰好有5个奇数和5个偶数,从中任取3个球,3个球编号之和为奇数与3个球编号之和为偶数的机会是均等的,故所求概率为.files/image296.gif) .
.
11.由平面向量的坐标表示可得:.files/image316.gif)
.files/image318.gif)
.files/image320.gif) 由
由.files/image322.gif) ,得
,得.files/image324.gif) .
.
12.由三视图知该几何体是底面为正方形的长方体,
显然①可能,②不可能,③④⑤如右图知都有可能。
13.在平面直角坐标系中,曲线.files/image162.gif) 和
和.files/image164.gif) 分别表示圆
分别表示圆.files/image326.gif) 和直线
和直线.files/image328.gif) ,易知
,易知.files/image168.gif) =
=.files/image298.gif)
14. 由.files/image331.gif) ,得
,得.files/image333.gif) 或8
或8
.files/image335.gif) 15.解法1:∵PA切
15.解法1:∵PA切.files/image176.gif) 于点A,B为PO中点,
于点A,B为PO中点,
∴AB=OB=OA, ∴.files/image337.gif) ,∴
,∴.files/image339.gif) ,在△POD中由余弦定理
,在△POD中由余弦定理
得.files/image341.gif) =
=.files/image343.gif)
∴.files/image345.gif) .
.
解法2:过点D作DE⊥PC垂足为E,∵.files/image339.gif) ,∴
,∴.files/image347.gif) ,可得
,可得.files/image349.gif) ,
,.files/image351.gif) ,在
,在.files/image353.gif) 中,∴
中,∴.files/image355.gif)
三.解答题:
16.解:(1).files/image357.gif)
.files/image359.gif)
.files/image361.gif)
.files/image363.gif) ------------------------4分
------------------------4分
(2)∵.files/image180.gif) ,
,.files/image182.gif)
∴.files/image365.gif) ,
,
由正弦定理得:.files/image367.gif)
∴.files/image369.gif) ------------6分
------------6分
如图过点B作.files/image371.gif) 垂直于对岸,垂足为D,则BD的长就是该河段的宽度。
垂直于对岸,垂足为D,则BD的长就是该河段的宽度。
在.files/image373.gif) 中,∵
中,∵.files/image375.gif) ,
,.files/image377.gif) ------------8分
------------8分
∴.files/image379.gif) =
=.files/image381.gif)
.files/image383.gif) (米)
(米)
∴该河段的宽度.files/image385.gif) 米。---------------------------12分
米。---------------------------12分
17.(1)解:∵.files/image192.gif)
∴.files/image387.gif) 且
且.files/image389.gif) ,
,
∴.files/image391.gif) 平面
平面.files/image393.gif) ------------ ----------------2分
------------ ----------------2分
.files/image188.gif) 在
在.files/image395.gif) 中,
中, .files/image397.gif) ,
,
.files/image399.gif) 中,
中,.files/image401.gif)
∵.files/image403.gif) ,
,
∴.files/image405.gif) .--------------4分
.--------------4分
(2)证法1:由(1)知SA=2, 在.files/image407.gif) 中,
中,.files/image409.gif) ---6分
---6分
∵.files/image411.gif) ,∴
,∴.files/image196.gif) -------------------8分
-------------------8分
证法2:由(1)知.files/image391.gif) 平面
平面.files/image393.gif) ,∵
,∵.files/image413.gif) 面
面.files/image393.gif) ,
,
∴.files/image416.gif) ,∵
,∵.files/image418.gif) ,
,.files/image420.gif) ,∴
,∴.files/image422.gif) 面
面.files/image424.gif)
又∵.files/image426.gif) 面
面.files/image424.gif) ,∴
,∴.files/image196.gif)
(3) 解法1:分别取AB、SA、 BC的中点D、E、F,
连结ED、DF、EF、AF,则.files/image429.gif) ,
,
∴.files/image431.gif) (或其邻补角)就是异面直线SB和AC所成的角----------10分
(或其邻补角)就是异面直线SB和AC所成的角----------10分
.files/image433.gif) ∵
∵.files/image435.gif)
在.files/image437.gif) 中,
中,.files/image439.gif)
∴.files/image441.gif) ,
,
在.files/image443.gif) 中,
中,.files/image445.gif)
在△DEF中,由余弦定理得.files/image447.gif)
.files/image449.gif)
∴异面直线SB和AC所成的角的余弦值为.files/image451.gif) -------------------------14分
-------------------------14分
解法2:以点A为坐标原点,AC所在的直线为y轴建立空间直角坐标系如图
则可得点A(0,0,0),C(0,1,0),B.files/image453.gif)
.files/image455.gif) ∴
∴.files/image457.gif)
设异面直线SB和AC所成的角为.files/image020.gif)
则.files/image460.gif)
∴异面直线SB和AC所成的角的余弦值为.files/image451.gif) 。
。
18.解:(1)依题意知,动点.files/image206.gif) 到定点
到定点.files/image200.gif)
.files/image202.gif) 的距离等于
的距离等于.files/image206.gif) 到直线
到直线.files/image464.gif) 的距离,曲线
的距离,曲线.files/image062.gif) 是以原点为顶点,
是以原点为顶点,.files/image200.gif)
.files/image202.gif) 为焦点的抛物线………………………………2分
为焦点的抛物线………………………………2分
.files/image467.gif) ∵
∵.files/image469.gif) ∴
∴.files/image471.gif)
∴ 曲线.files/image062.gif) 方程是
方程是.files/image474.gif) ………4分
………4分
(2)设圆的圆心为.files/image476.gif) ,∵圆
,∵圆.files/image209.gif) 过
过.files/image008.gif)
.files/image212.gif) ,
,
∴圆的方程为 .files/image479.gif) ……………………………7分
……………………………7分
令.files/image481.gif) 得:
得:.files/image483.gif)
设圆与.files/image204.gif) 轴的两交点分别为
轴的两交点分别为.files/image486.gif) ,
,.files/image488.gif)
方法1:不妨设.files/image490.gif)
.files/image492.gif) ,由求根公式得
,由求根公式得
.files/image494.gif) ,
,.files/image496.gif) …………………………10分
…………………………10分
∴.files/image498.gif)
又∵点.files/image476.gif) 在抛物线
在抛物线.files/image474.gif) 上,∴
上,∴.files/image500.gif) ,
,
∴ .files/image502.gif) ,即
,即.files/image217.gif) =4--------------------------------------------------------13分
=4--------------------------------------------------------13分
∴当.files/image209.gif) 运动时,弦长
运动时,弦长.files/image217.gif) 为定值4…………………………………………………14分
为定值4…………………………………………………14分
〔方法2:∵.files/image504.gif) ,
,.files/image506.gif)
∴.files/image492.gif)
.files/image508.gif)
.files/image510.gif)
又∵点.files/image476.gif) 在抛物线
在抛物线.files/image474.gif) 上,∴
上,∴.files/image500.gif) , ∴
, ∴ .files/image512.gif)
.files/image514.gif)
∴当.files/image209.gif) 运动时,弦长
运动时,弦长.files/image217.gif) 为定值4〕
为定值4〕
19.解:设AN的长为x米(x >2)
∵.files/image516.gif) ,∴|AM|=
,∴|AM|=.files/image518.gif)
∴SAMPN=|AN|•|AM|=.files/image520.gif) ------------------------------------- 4分
------------------------------------- 4分
(1)由SAMPN > 32 得 .files/image520.gif) > 32 ,
> 32 ,
∵x >2,∴.files/image522.gif) ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴.files/image524.gif) 即AN长的取值范围是
即AN长的取值范围是.files/image526.gif) ----------- 8分
----------- 8分
(2)令y=.files/image520.gif) ,则y′=
,则y′=.files/image528.gif) -------------- 10分
-------------- 10分
∵当.files/image530.gif) ,y′< 0,∴函数y=
,y′< 0,∴函数y=.files/image520.gif) 在
在.files/image532.gif) 上为单调递减函数,
上为单调递减函数,
∴当x=3时y=.files/image520.gif) 取得最大值,即
取得最大值,即.files/image534.gif) (平方米)
(平方米)
此时|AN|=.files/image536.gif) 米
---------------------- 12分
米
---------------------- 12分
20.解:(1)由.files/image224.gif) 得
得.files/image538.gif) ----------------------------------------1分
----------------------------------------1分
由一元二次方程求根公式得.files/image540.gif)
.files/image542.gif) ---------------------------3分
---------------------------3分
∵.files/image226.gif)
∴.files/image545.gif) ---------------------------------------------4分
---------------------------------------------4分
(2) ∵.files/image545.gif)
∴.files/image542.gif)
.files/image547.gif)
.files/image549.gif)
=.files/image551.gif) ------------------------------------------------------------6分
------------------------------------------------------------6分
∵.files/image553.gif)
.files/image555.gif)
∴.files/image228.gif) ------------------------------------------------------------------------8分
------------------------------------------------------------------------8分
(其它证法请参照给分)
(3)解法1:∵ .files/image545.gif)
∴.files/image558.gif)
.files/image560.gif)
.files/image562.gif) =-------------------------------------------------10分
=-------------------------------------------------10分
∵.files/image564.gif) ,∴
,∴.files/image566.gif)
∴.files/image568.gif) ,∵
,∵.files/image226.gif)
∴.files/image571.gif) 即
即.files/image573.gif)
∴数列.files/image222.gif) 有最大项,最大项为第一项
有最大项,最大项为第一项.files/image575.gif) 。---------- -14分
。---------- -14分
〔解法2:由.files/image545.gif) 知数列
知数列.files/image222.gif) 各项满足函数
各项满足函数.files/image577.gif)
∵.files/image579.gif)
当.files/image581.gif) 时,
时,.files/image583.gif)
∴当.files/image581.gif) 时
时.files/image586.gif) ,即函数
,即函数.files/image577.gif) 在
在.files/image588.gif) 上为减函数
上为减函数
即有.files/image573.gif)
∴数列.files/image222.gif) 有最大项,最大项为第一项
有最大项,最大项为第一项.files/image575.gif) 。]
。]
21.解:
(1).files/image590.gif)
.files/image592.gif)
.files/image594.gif) ---------------2分
---------------2分
当.files/image596.gif) 时
时.files/image598.gif) ,函数
,函数.files/image234.gif) 有一个零点;--------------3分
有一个零点;--------------3分
当.files/image600.gif) 时,
时,.files/image602.gif) ,函数
,函数.files/image234.gif) 有两个零点。------------4分
有两个零点。------------4分
(2)令.files/image604.gif) ,则
,则
.files/image606.gif)
.files/image608.gif) ,
,
.files/image610.gif)
.files/image612.gif) 在
在.files/image614.gif) 内必有一个实根。即
内必有一个实根。即.files/image242.gif) ,使
,使.files/image244.gif) 成立。------------8分
成立。------------8分
(3)
假设.files/image257.gif) 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且.files/image616.gif)
∴.files/image618.gif)
.files/image620.gif)
.files/image622.gif) -------------------------10分
-------------------------10分
由②知对.files/image253.gif) ,都有
,都有.files/image255.gif)
令.files/image328.gif) 得
得.files/image625.gif)
.files/image627.gif)
.files/image629.gif)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com