
题目列表(包括答案和解析)
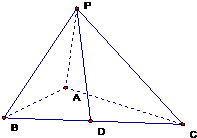 棱锥的底面是正三角形,边长为1,棱锥的一条侧棱与底面垂直,其余两条侧棱与底面所成角都等于
棱锥的底面是正三角形,边长为1,棱锥的一条侧棱与底面垂直,其余两条侧棱与底面所成角都等于 ,设D为BC中点.
,设D为BC中点. ,设D为BC中点.
,设D为BC中点.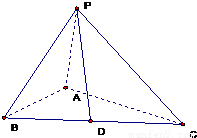




 ?
?
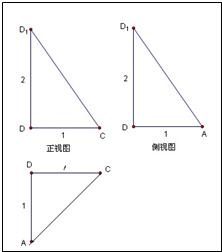 一个三棱锥的三视图如图所示,其中正视图和侧视图是两条直角边分别是1和2的两个全等的直角三角形,俯视图是直角边长为1的等腰直角三角形.
一个三棱锥的三视图如图所示,其中正视图和侧视图是两条直角边分别是1和2的两个全等的直角三角形,俯视图是直角边长为1的等腰直角三角形.
一、选择题: 1.B 2.B 3.D 4.C 5.C 6.C 7.D 8.A 9.C 10.B
二、填空题: 11. 12.
12. 13.
13. 14.
14. 15.1
15.1
三、解答题:
16.解: (Ⅰ)解: ,
, (1分)
(1分)
 (3分)
(3分)
 (4分)
(4分)

 (6分)
(6分)
(Ⅱ)解: (7分)
(7分)
由  得
得 (8分)
(8分)
由  得
得 (9分)
(9分)
 (11分)
(11分)
 (12分)
(12分)
17解: 设矩形温室的左侧边长为am,后侧边长为bm,则ab=800m2. (2分)
∴蔬菜的种植面积 , (5分)
, (5分)
∵ ,
,
∴ ,
(7分)
,
(7分)
∴ (m2),
(9分)
(m2),
(9分)
当且仅当 ,即
,即 时,
时, m2.
(11分)
m2.
(11分)
答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648 m2. (12分)
 18解:(Ⅰ)证明:
18解:(Ⅰ)证明:
 ,
,
∴ ,则
,则 (2分)
(2分)
又
 ,则
,则
∴ (4分)
(4分)
(Ⅱ)证明:依题意可知: 是
是 中点
中点

 则
则 ,而
,而
∴ 是
是 中点 (6分)
中点 (6分)
在 中,
中,
∴ (8分)
(8分)
(Ⅲ)解:

∴ ,而
,而
∴ ∴
∴ (10分)
(10分)

 是
是 中点
中点
∴ 是
是 中点 ∴
中点 ∴
 且
且


∴
∴ 中,
中,
∴ (12分)
(12分)
∴ (14分)
(14分)
19解: 圆C化成标准方程为: (2分)
(2分)
假设存在以AB为直径的圆M,圆心M的坐标为(a,b)
由于 ① (5分)
① (5分)
直线 的方程为
的方程为 (6分)
(6分)
 (7分)
(7分)

即: ② (10分)
② (10分)
由①②得: (11分)
(11分)
当 (12分)
(12分)
当 (13分)
(13分)
故这样的直线l 是存在的,方程为x-y+4=0或x-y+1=0. (14分)
20解: 解(Ⅰ) al0=10, a20=10+10d=40, ∴d=3 (2分)
(Ⅱ) a30= a20+10d=10(1+d+d2) (d≠0) (4分)
a30=10[(d+ )2+
)2+ ],
],
当d∈(-∞,
0)∪(0, +∞)时,
a30∈[ ,+∞].
(7分)
,+∞].
(7分)
(Ⅲ) 续写数列: 数列a30,a31,…,a40是公差为d4的等差数列 (8分)
一般地,可推广为:无穷数列{ an},其中al,a2…,a10是首项为1公差为1的等差数列,
当n≥1时, 数列a10n,a10n+1,…,a10(n+1)是公差为dn的等差数列. (9分)
研究的问题可以是:试写出a10(n+1)关于d的关系式,并求a10(n+1)的取值范围 (11分)
研究的结论可以是: 由a40= a30+10d3=10(1+d+d2+ d3),
 依次类推可得
a10(n+1)= 10(1+d+d2+…+ dn)= 10?
依次类推可得
a10(n+1)= 10(1+d+d2+…+ dn)= 10? (d≠1),
(d≠1),
10(n+1) (d=1)
当d>0时, a10(n+1)的取值范围为(10, +∞)等 (14分)
21解:(Ⅰ)由 过点P且以P(1,-2)为切点的直线的斜率
过点P且以P(1,-2)为切点的直线的斜率 ,
,
 所求直线方程:
所求直线方程: (3分)
(3分)
(Ⅱ)设过P(1,-2)的直线l与 切于另一点
切于另一点
知:
即:
或 故所求直线的斜率为:
故所求直线的斜率为:

即 (8分)
(8分)
(Ⅲ)由(Ⅱ)可知 则
则

在 上单调递增, (11分)
上单调递增, (11分)
在
得
 为两极值点,在
为两极值点,在 时,
时,
 上单调递增,
上单调递增,
即
 (14分)
(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com