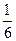2,4,6
2,4,6 三、解答题 17.(本小题满分12分) 解证:(I).files/image160.gif) 由余弦定理得.files/image162.gif) …………4分 …………4分 又.files/image164.gif) …………6分 …………6分 (II).files/image166.gif) .files/image168.gif) …………10分 …………10分 .files/image170.gif) 即函数的值域是.files/image172.gif) …………12分 …………12分 18.(本小题满分12分) 解:(I)依题意.files/image174.gif) .files/image176.gif) …………2分 …………2分 .files/image178.gif) .files/image180.gif) …………4分 …………4分 .files/image182.gif) …………5分 …………5分 (II).files/image184.gif) …………6分 …………6分 .files/image186.gif) …………7分 …………7分
.files/image188.gif) …………9分 …………9分
.files/image190.gif)
.files/image192.gif) …………12分 …………12分
19.(本小题满分12分) (I)证明:依题意知:.files/image194.gif) .files/image196.gif) …………2分 …………2分 .files/image198.gif) …4分 …4分 (II)由(I)知.files/image200.gif) 平面ABCD 平面ABCD ∴平面PAB⊥平面ABCD. …………4分 在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD, 设MN=h 则.files/image202.gif) .files/image204.gif) …………6分 …………6分 要使.files/image206.gif) 即M为PB的中点. …………8分
.files/image208.jpg)
建立如图所示的空间直角坐标系 则A(0,0,0),B(0,2,0), C(1,1,0),D(1,0,0), P(0,0,1),M(0,1,.files/image156.gif) ) ) 由(I)知平面.files/image210.gif) ,则 ,则 .files/image212.gif) 的法向量。 …………10分 的法向量。 …………10分 又.files/image214.gif) 为等腰 为等腰.files/image216.gif) .files/image218.gif) 因为.files/image220.gif) 所以AM与平面PCD不平行. …………12分 20.(本小题满分12分) 解:(I)已知.files/image222.gif) , , 只须后四位数字中出现2个0和2个1. .files/image224.gif) …………4分 …………4分 (II).files/image145.gif) 的取值可以是1,2,3,4,5,. 的取值可以是1,2,3,4,5,. .files/image227.gif) .files/image229.gif) …………8分 …………8分 .files/image231.gif) 的分布列是 的分布列是 .files/image145.gif) 1 2 3 4 5 P .files/image234.gif)
.files/image236.gif)
.files/image238.gif)
.files/image240.gif)
.files/image242.gif)
…………10分 .files/image244.gif) …………12分 …………12分 (另解:记.files/image246.gif) .files/image248.gif) .) .) 21.(本小题满分12分) 解:(I)设M.files/image250.gif) , , 由.files/image252.gif) 于是,分别过A、B两点的切线方程为 .files/image254.gif) ① ① .files/image256.gif) ② …………2分 ② …………2分 解①②得.files/image258.gif) ③ …………4分 ③ …………4分 设直线l的方程为.files/image260.gif) 由.files/image262.gif) .files/image264.gif) ④ …………6分 ④ …………6分 ④代入③得.files/image266.gif) 即M.files/image268.gif) 故M的轨迹方程是.files/image270.gif) …………7分 …………7分 (II).files/image272.gif) .files/image274.gif) .files/image276.gif) …………9分 …………9分 (III).files/image278.gif) .files/image280.gif) 的面积S最小,最小值是4 …………11分 的面积S最小,最小值是4 …………11分 此时,直线l的方程为y=1 …………12分 22.(本小题满分14分) 解:(I).files/image282.gif) …………2分 …………2分 由.files/image284.gif) …………4分 …………4分 .files/image286.gif) 当.files/image288.gif) 的单调增区间是 的单调增区间是.files/image290.gif) ,单调减区间是 ,单调减区间是 .files/image292.gif) …………6分 …………6分 当.files/image294.gif) 的单调增区间是 的单调增区间是.files/image296.gif) ,单调减区间是 ,单调减区间是 .files/image298.gif) …………8分 …………8分 (II)当.files/image300.gif) 上单调递增,因此 上单调递增,因此 .files/image302.gif) …………10分 .files/image304.gif) 上单调递减, 上单调递减, 所以值域是.files/image306.gif) …………12分 …………12分 因为在.files/image308.gif) …………13分 所以,a只须满足.files/image310.gif) 解得.files/image312.gif) 即当.files/image314.gif) 、 、.files/image316.gif) 使得 使得.files/image318.gif) 成立. 成立. …………14分
| | | | | |

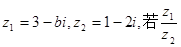 是实数,则实数b的值为(
)
是实数,则实数b的值为(
)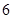 B.
B.
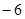
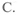 0
D.
0
D. 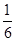
![]() 是实数,则实数b的值为( )
是实数,则实数b的值为( )![]() C.0 D.
C.0 D. ![]()
![]() 是实数,则实数b的值为( )
是实数,则实数b的值为( )![]() C.0 D.
C.0 D. ![]()
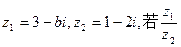 是实数,则实数b的值为( )
是实数,则实数b的值为( )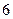 B.
B.
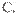 0 D.
0 D.