
题目列表(包括答案和解析)

A.求数列{ }的前10项和(n∈N*) }的前10项和(n∈N*) |
B.求数列{ }的前10项和(n∈N*) }的前10项和(n∈N*) |
C.求数列{ }的前11项和(n∈N*) }的前11项和(n∈N*) |
D.求数列{ }的前11项和(n∈N*) }的前11项和(n∈N*) |
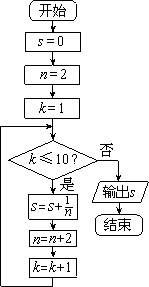
如图所示,程序框图的功能是
A.求数列{![]() }的前10项和(n∈N*)
}的前10项和(n∈N*)
B.求数列{![]() }的前10项和(n∈N*)
}的前10项和(n∈N*)
C.求数列{![]() }的前11项和(n∈N*)
}的前11项和(n∈N*)
D.求数列{![]() }的前11项和(n∈N*)
}的前11项和(n∈N*)
如图所示,程序框图的功能是( )
A.求数列{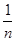 }的前10项和(n∈N*) }的前10项和(n∈N*) |
B.求数列{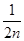 }的前10项和(n∈N*) }的前10项和(n∈N*) |
C.求数列{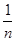 }的前11项和(n∈N*) }的前11项和(n∈N*) |
D.求数列{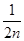 }的前11项和(n∈N*) }的前11项和(n∈N*) |
设![]() ,利用课本中推导等差数列前
,利用课本中推导等差数列前![]() 项和公式的方法,可求得f(-12)+f(-11)+f(-10)+…+f(0)+…+f(12)+f(13)的值是
项和公式的方法,可求得f(-12)+f(-11)+f(-10)+…+f(0)+…+f(12)+f(13)的值是
A.![]()
B.![]()
C.![]()
D.![]()
已知程序框图如图所示,则该程序框图的功能是( )
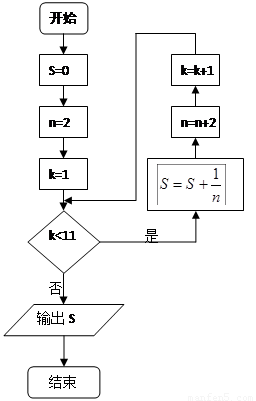
A.求数列 的前10项和(n∈N*)
B.求数列
的前10项和(n∈N*)
B.求数列 的前11项和(n∈N*)
的前11项和(n∈N*)
C.求数列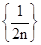 的前10项和(n∈N*)
D.求数列
的前10项和(n∈N*)
D.求数列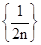 的前11项和(n∈N*)
的前11项和(n∈N*)
一、选择题
1.D 2.B 3.B 4.B 5.A 6.B 7.C 8.B 9.C 10.A 11.B 12.D
|