
题目列表(包括答案和解析)
选做题(请从A、B和C三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答,则按A、B两小题评分.)
A.(选修模块3-3)(12分)
⑴下列说法中正确的是 ▲
A.液体表面层分子间距离大于液体内部分子间距离,液体表面存在张力
B.扩散运动就是布朗运动
C.蔗糖受潮后会粘在一起,没有确定的几何形状,它是非晶体
D.对任何一类与热现象有关的宏观自然过程进行方向的说明,都可以作为热力学第二定律的表述
 ⑵将1ml的纯油酸加到500ml的酒精中,待均匀溶解后,用滴管取1ml油酸酒精溶液,让其自然滴出,共200滴.现在让其中一滴落到盛水的浅盘内,待油膜充分展开后,测得油膜的面积为200cm2,则估算油酸分子的大小是 ▲ m(保留一位有效数字).
⑵将1ml的纯油酸加到500ml的酒精中,待均匀溶解后,用滴管取1ml油酸酒精溶液,让其自然滴出,共200滴.现在让其中一滴落到盛水的浅盘内,待油膜充分展开后,测得油膜的面积为200cm2,则估算油酸分子的大小是 ▲ m(保留一位有效数字).
⑶如图所示,一直立的汽缸用一质量为m的活塞封闭一定量的理想气体,活塞横截面积为S,汽缸内壁光滑且缸壁是导热的,开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,已知AB=h,大气压强为p0,重力加速度为g.
①求活塞停在B点时缸内封闭气体的压强;
②设周围环境温度保持不变,求整个过程中通过缸壁传递的热量Q(一定量理想气体的内能仅由温度决定).
B.(选修3-4试题)
⑴(4分)下列说法正确的是 ▲
A.泊松亮斑有力地支持了光的微粒说,杨氏干涉实验有力地支持了光的波动说。
B.从接收到的高频信号中还原出所携带的声音或图像信号的过程称为解调
C.当波源或者接受者相对于介质运动时,接受者往往会发现波的频率发生了变化,这种现象叫多普勒效应。
D.考虑相对论效应,一条沿自身长度方向运动的杆,其长度总比杆静止时的长度小
⑵如图所示,真空中有一顶角为75o,折射率为n =![]() 的三棱镜.欲使光线从棱镜的侧面AB进入,再直接从侧面AC射出,求入射角θ的取值范围为 ▲ 。
的三棱镜.欲使光线从棱镜的侧面AB进入,再直接从侧面AC射出,求入射角θ的取值范围为 ▲ 。

⑶(4分) 一列向右传播的简谐横波在某时刻的波形图如图所示。波速大小为0.6m/s,P质点的横坐标x = 96cm。求:
①波源O点刚开始振动时的振动方向和波的周期;
②从图中状态为开始时刻,质点P第一次达到波峰时间。
C.(选修模块3-5)(12分)
 ⑴.氦原子被电离一个核外电子,形成类氢结构的氦离子。已知基态的氦离子能量为E1 =-54.4eV,氦离子能级的示意图如图所示。在具有下列能量的光子中,不能被基态氦离子吸收的是 ▲
⑴.氦原子被电离一个核外电子,形成类氢结构的氦离子。已知基态的氦离子能量为E1 =-54.4eV,氦离子能级的示意图如图所示。在具有下列能量的光子中,不能被基态氦离子吸收的是 ▲
A.60.3eV B. 51.0 eV
C.43.2eV D.54.4 eV
⑵一个静止的![]() ,放出一个速度为2.22×107m/s的粒子,同时产生一个新核
,放出一个速度为2.22×107m/s的粒子,同时产生一个新核![]() ,并释放出频率为ν=3×1019Hz的γ光子。写出这种核反应方程式 ▲ ;这个核反应中产生的新核的速度为 ▲ ;因γ辐射而引起的质量亏损为 ▲ 。(已知普朗克常量h=6.63×10-34J·s)
,并释放出频率为ν=3×1019Hz的γ光子。写出这种核反应方程式 ▲ ;这个核反应中产生的新核的速度为 ▲ ;因γ辐射而引起的质量亏损为 ▲ 。(已知普朗克常量h=6.63×10-34J·s)
 ⑶如图,滑块A、B的质量分别为m1与m2,m1<m2,置于光滑水平面上,由轻质弹簧相连接,用一轻绳把两滑块拉至最近,弹簧处于最大压缩状态后绑紧,接着使两滑块一起以恒定的速度v0向右滑动.运动中某时刻轻绳突然断开,当弹簧恢复到其自然长度时,滑块A的速度正好为零。则:
⑶如图,滑块A、B的质量分别为m1与m2,m1<m2,置于光滑水平面上,由轻质弹簧相连接,用一轻绳把两滑块拉至最近,弹簧处于最大压缩状态后绑紧,接着使两滑块一起以恒定的速度v0向右滑动.运动中某时刻轻绳突然断开,当弹簧恢复到其自然长度时,滑块A的速度正好为零。则:
①弹簧第一次恢复到自然长度时,滑块B的速度大小为 ▲ ;
②从轻绳断开到弹簧第一次恢复到自然长度的过程中,弹簧释放的弹性势能Ep = ▲ 。
选做题(请从A、B和C三小题中选定两小题作答,并在答题卡上把所选题目对应字母后的方框涂满涂黑.如都作答,则按A、B两小题评分.)
A.(选修模块3-3)(12分)
⑴下列说法中正确的是 ▲
A.液体表面层分子间距离大于液体内部分子间距离,液体表面存在张力
B.扩散运动就是布朗运动
C.蔗糖受潮后会粘在一起,没有确定的几何形状,它是非晶体
D.对任何一类与热现象有关的宏观自然过程进行方向的说明,都可以作为热力学第二定律的表述
 ⑵将1ml的纯油酸加到500ml的酒精中,待均匀溶解后,用滴管取1ml油酸酒精溶液,让其自然滴出,共200滴.现在让其中一滴落到盛水的浅盘内,待油膜充分展开后,测得油膜的面积为200cm2,则估算油酸分子的大小是 ▲ m(保留一位有效数字).
⑵将1ml的纯油酸加到500ml的酒精中,待均匀溶解后,用滴管取1ml油酸酒精溶液,让其自然滴出,共200滴.现在让其中一滴落到盛水的浅盘内,待油膜充分展开后,测得油膜的面积为200cm2,则估算油酸分子的大小是 ▲ m(保留一位有效数字).
⑶如图所示,一直立的汽缸用一质量为m的活塞封闭一定量的理想气体,活塞横截面积为S,汽缸内壁光滑且缸壁是导热的,开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,已知AB=h,大气压强为p0,重力加速度为g.
①求活塞停在B点时缸内封闭气体的压强;
②设周围环境温度保持不变,求整个过程中通过缸壁传递的热量Q(一定量理想气体的内能仅由温度决定).
B.(选修3-4试题)
⑴(4分)下列说法正确的是 ▲
A.泊松亮斑有力地支持了光的微粒说,杨氏干涉实验有力地支持了光的波动说。
B.从接收到的高频信号中还原出所携带的声音或图像信号的过程称为解调
C.当波源或者接受者相对于介质运动时,接受者往往会发现波的频率发生了变化,这种现象叫多普勒效应。
D.考虑相对论效应,一条沿自身长度方向运动的杆,其长度总比杆静止时的长度小
⑵如图所示,真空中有一顶角为75o,折射率为n = 的三棱镜.欲使光线从棱镜的侧面AB进入,再直接从侧面AC射出,求入射角θ的取值范围为 ▲ 。
的三棱镜.欲使光线从棱镜的侧面AB进入,再直接从侧面AC射出,求入射角θ的取值范围为 ▲ 。

⑶(4分) 一列向右传播的简谐横波在某时刻的波形图如图所示。波速大小为0.6m/s,P质点的横坐标x = 96cm。求:
①波源O点刚开始振动时的振动方向和波的周期;
②从图中状态为开始时刻,质点P第一次达到波峰时间。
C.(选修模块3-5)(12分)
 ⑴.氦原子被电离一个核外电子,形成类氢结构的氦离子。已知基态的氦离子能量为E1 =-54.4
eV,氦离子能级的示意图如图所示。在具有下列能量的光子中,不能被基态氦离子吸收的是 ▲
⑴.氦原子被电离一个核外电子,形成类氢结构的氦离子。已知基态的氦离子能量为E1 =-54.4
eV,氦离子能级的示意图如图所示。在具有下列能量的光子中,不能被基态氦离子吸收的是 ▲
A.60.3 eV B. 51.0 eV
C.43.2 eV D.54.4 eV
⑵一个静止的 ,放出一个速度为2.22×107m/s的粒子,同时产生一个新核
,放出一个速度为2.22×107m/s的粒子,同时产生一个新核 ,并释放出频率为ν=3×1019Hz的γ光子。写出这种核反应方程式
▲ ;这个核反应中产生的新核的速度为 ▲ ;因γ辐射而引起的质量亏损为 ▲ 。(已知普朗克常量h=6.63×10-34J·s)
,并释放出频率为ν=3×1019Hz的γ光子。写出这种核反应方程式
▲ ;这个核反应中产生的新核的速度为 ▲ ;因γ辐射而引起的质量亏损为 ▲ 。(已知普朗克常量h=6.63×10-34J·s)
 ⑶如图,滑块A、B的质量分别为m1与m2,m1<m2,置于光滑水平面上,由轻质弹簧相连接,用一轻绳把两滑块拉至最近,弹簧处于最大压缩状态后绑紧,接着使两滑块一起以恒定的速度v0向右滑动.运动中某时刻轻绳突然断开,当弹簧恢复到其自然长度时,滑块A的速度正好为零。则:
⑶如图,滑块A、B的质量分别为m1与m2,m1<m2,置于光滑水平面上,由轻质弹簧相连接,用一轻绳把两滑块拉至最近,弹簧处于最大压缩状态后绑紧,接着使两滑块一起以恒定的速度v0向右滑动.运动中某时刻轻绳突然断开,当弹簧恢复到其自然长度时,滑块A的速度正好为零。则:
①弹簧第一次恢复到自然长度时,滑块B的速度大小为 ▲ ;
②从轻绳断开到弹簧第一次恢复到自然长度的过程中,弹簧释放的弹性势能Ep = ▲ 。
 .则光束从上表面进入玻璃砖的折射角为______,光在玻璃砖中的传播的时间为______.
.则光束从上表面进入玻璃砖的折射角为______,光在玻璃砖中的传播的时间为______. )经过α、β衰变形成稳定的铅(
)经过α、β衰变形成稳定的铅( ),问在这一变化过程中,共转变为质子的中子数是______个.
),问在这一变化过程中,共转变为质子的中子数是______个.
如图所示,半径R=0.8 m的1/4光滑圆弧轨道固定在竖直平面内,过最低点的半径OC处于竖直位置,在其右方有一可绕竖直轴MN(与圆弧轨道共面)转动的,内部空心的圆筒,圆筒半径r=0.1![]() m,筒的顶端与C点等高,在筒的下部有一小孔,距筒顶h=0.8 m,开始时小孔在图示位置(与圆弧轨道共面).现让一质量m=0.1 kg的小物块自A点由静止开始下落,打在圆弧轨道上的B点,但未反弹,在瞬间的碰撞过程中小物块沿半径方向的分速度立刻减为零,而沿圆弧切线方向的分速度不变.此后,小物块沿圆弧轨道滑下,到达C点时触动光电装置,使圆筒立刻以某一角速度匀速转动起来,且小物块最终正好进入小孔.已知A点、B点到圆心O的距离均为R,与水平方向的夹角θ均为30°,不计空气阻力,g取10 m/s2.试问:
m,筒的顶端与C点等高,在筒的下部有一小孔,距筒顶h=0.8 m,开始时小孔在图示位置(与圆弧轨道共面).现让一质量m=0.1 kg的小物块自A点由静止开始下落,打在圆弧轨道上的B点,但未反弹,在瞬间的碰撞过程中小物块沿半径方向的分速度立刻减为零,而沿圆弧切线方向的分速度不变.此后,小物块沿圆弧轨道滑下,到达C点时触动光电装置,使圆筒立刻以某一角速度匀速转动起来,且小物块最终正好进入小孔.已知A点、B点到圆心O的距离均为R,与水平方向的夹角θ均为30°,不计空气阻力,g取10 m/s2.试问:
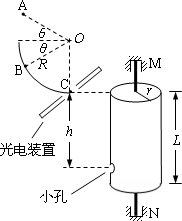
(1)小物块到达C点时的速度大小是多少?
(2)圆筒匀速转动时的角速度是多少?
(3)要使小物块进入小孔后能直接打到圆筒的内侧壁,筒身长 L至少为多少?
 【物理--选修3-5】
【物理--选修3-5】
一、填空题
1.-----理科数学.files/image208.gif) 2.
2. -----理科数学.files/image210.gif) 3.2 4.
3.2 4.-----理科数学.files/image212.gif) 5. i
5. i-----理科数学.files/image214.gif) 100 6.
100 6.-----理科数学.files/image216.gif) 7. 2
7. 2
8. -----理科数学.files/image218.gif) 9.
9. -----理科数学.files/image220.gif) 10.
10. -----理科数学.files/image222.gif) 11.
11. -----理科数学.files/image224.gif) 12.
12.-----理科数学.files/image226.gif)
二、选择题
13. -----理科数学.files/image228.gif) 14.A 15.A. 16. D
14.A 15.A. 16. D
三、解答题
17.
(1)由题意可得:-----理科数学.files/image106.gif) =5----------------------------------------------------------(2分)
=5----------------------------------------------------------(2分)
由:-----理科数学.files/image230.gif) 得:
得:-----理科数学.files/image111.gif) =314---------------------------------------(4分)
=314---------------------------------------(4分)
或:-----理科数学.files/image232.gif) ,
,-----理科数学.files/image234.gif)
(2)方法一:由:-----理科数学.files/image236.gif) 或
或-----理科数学.files/image238.gif) ------(1分)
------(1分)
-----理科数学.files/image240.gif) 或
或-----理科数学.files/image242.gif) ---------(1分)
---------(1分)
得:-----理科数学.files/image244.gif) 0.0110-----------------------------------------------------------------(1分)
0.0110-----------------------------------------------------------------(1分)
方法二:由:-----理科数学.files/image246.gif)
得:-----理科数学.files/image248.gif) -----------------------------------------------------------------(1分)
-----------------------------------------------------------------(1分)
由:-----理科数学.files/image113.gif) 点和
点和-----理科数学.files/image115.gif) 点的纵坐标相等,可得
点的纵坐标相等,可得-----理科数学.files/image113.gif) 点和
点和-----理科数学.files/image115.gif) 点关于
点关于-----理科数学.files/image133.gif) 点对称
点对称
即:-----理科数学.files/image253.gif) ------------------------------------------------------------(1分)
------------------------------------------------------------(1分)
得:-----理科数学.files/image244.gif) 0.011-----------------------------------------------------------------------(1分)
0.011-----------------------------------------------------------------------(1分)
18.(1)-----理科数学.files/image255.gif) ,
,-----理科数学.files/image257.gif) 是等腰三角形,
是等腰三角形,
-----理科数学.files/image259.jpg) 又
又-----理科数学.files/image133.gif) 是
是-----理科数学.files/image135.gif) 的中点,
的中点,-----理科数学.files/image263.gif) ,--------------(1分)
,--------------(1分)
又-----理科数学.files/image265.gif) 底面
底面-----理科数学.files/image267.gif) .
.-----理科数学.files/image269.gif) .----(2分)
.----(2分)
-----理科数学.files/image271.gif) -------------------------------(1分)
-------------------------------(1分)
于是-----理科数学.files/image273.gif) 平面
平面-----理科数学.files/image143.gif) .----------------------(1分)
.----------------------(1分)
(2)过-----理科数学.files/image228.gif) 作
作-----理科数学.files/image277.gif) ,连接
,连接-----理科数学.files/image279.gif) ----------------(1分)
----------------(1分)
-----理科数学.files/image281.gif) 平面
平面-----理科数学.files/image143.gif) ,
,
-----理科数学.files/image284.gif) ,-----------------------------------(1分)
,-----------------------------------(1分)
-----理科数学.files/image286.gif) 平面
平面-----理科数学.files/image147.gif) ,---------------------------(1分)
,---------------------------(1分)
-----理科数学.files/image289.gif) 就是直线
就是直线-----理科数学.files/image145.gif) 与平面
与平面-----理科数学.files/image147.gif) 所成角。---(2分)
所成角。---(2分)
在-----理科数学.files/image291.gif) 中,
中,-----理科数学.files/image293.gif)
-----理科数学.files/image295.gif) ----------------------------------(2分)
----------------------------------(2分)
所以,直线-----理科数学.files/image145.gif) 与平面
与平面-----理科数学.files/image147.gif) 所成角
所成角-----理科数学.files/image297.gif) --------(1分)
--------(1分)
19.解:
(1)函数-----理科数学.files/image158.gif) 的定义域为
的定义域为-----理科数学.files/image299.gif) ;------------------------------------(1分)
;------------------------------------(1分)
当-----理科数学.files/image301.gif) 时
时-----理科数学.files/image303.gif) ;当
;当-----理科数学.files/image305.gif) 时
时-----理科数学.files/image303.gif) ;--------------------------------------------------(1分)
;--------------------------------------------------(1分)
所以,函数-----理科数学.files/image158.gif) 在定义域
在定义域-----理科数学.files/image299.gif) 上不是单调函数,------------------(1分)
上不是单调函数,------------------(1分)
所以它不是“-----理科数学.files/image106.gif) 类函数” ------------------------------------------------------------------(1分)
类函数” ------------------------------------------------------------------(1分)
(2)当-----理科数学.files/image162.gif) 小于0时,则函数
小于0时,则函数-----理科数学.files/image160.gif) 不构成单调函数;(1分)
不构成单调函数;(1分)
当-----理科数学.files/image162.gif) =0时,则函数
=0时,则函数-----理科数学.files/image308.gif) 单调递增,
单调递增,
但在-----理科数学.files/image299.gif) 上不存在定义域是
上不存在定义域是-----理科数学.files/image152.gif) 值域也是
值域也是-----理科数学.files/image152.gif) 的区间
的区间-----理科数学.files/image152.gif) ---------------(1分)
---------------(1分)
当-----理科数学.files/image162.gif) 大于0时,函数
大于0时,函数-----理科数学.files/image160.gif) 在定义域里单调递增,----(1分)
在定义域里单调递增,----(1分)
要使函数-----理科数学.files/image160.gif) 是“
是“-----理科数学.files/image106.gif) 类函数”,
类函数”,
即存在两个不相等的常数-----理科数学.files/image310.gif) ,
,-----理科数学.files/image312.gif)
使得-----理科数学.files/image314.gif) 同时
同时-----理科数学.files/image316.gif) 成立,------------------------------------(1分)
成立,------------------------------------(1分)
即关于-----理科数学.files/image077.gif) 的方程
的方程-----理科数学.files/image319.gif) 有两个不相等的实根,--------------------------------(2分)
有两个不相等的实根,--------------------------------(2分)
-----理科数学.files/image321.gif) ,--------------------------------------------------------------------------(1分)
,--------------------------------------------------------------------------(1分)
亦即直线-----理科数学.files/image323.gif) 与曲线
与曲线-----理科数学.files/image325.gif) 在
在-----理科数学.files/image299.gif) 上有两个不同的交点,-(1分)
上有两个不同的交点,-(1分)
所以,-----理科数学.files/image327.gif) -------------------------------------------------------------------------------(2分)
-------------------------------------------------------------------------------(2分)
20.解:
(1)-----理科数学.files/image329.gif)
-----理科数学.files/image331.gif)
若-----理科数学.files/image333.gif) ,由
,由-----理科数学.files/image335.gif) ,得数列
,得数列-----理科数学.files/image173.gif) 构成等比数列------------------(3分)
构成等比数列------------------(3分)
若-----理科数学.files/image337.gif) ,
,-----理科数学.files/image339.gif) ,数列
,数列-----理科数学.files/image173.gif) 不构成等比数列--------------------------------------(1分)
不构成等比数列--------------------------------------(1分)
(2)由-----理科数学.files/image341.gif) ,得:
,得:-----理科数学.files/image343.gif) -------------------------------------(1分)
-------------------------------------(1分)
-----理科数学.files/image345.gif) ---------------------------------------------------------(1分)
---------------------------------------------------------(1分)
-----理科数学.files/image347.gif) ----------------------------------------------(1分)
----------------------------------------------(1分)
-----理科数学.files/image349.gif)
-----理科数学.files/image351.gif)
-----理科数学.files/image353.gif) ----(1分)
----(1分)
-----理科数学.files/image355.gif) ------------------------------------------------------------------(1分)
------------------------------------------------------------------(1分)
-----理科数学.files/image357.gif) ---------------------------------------------------------------------(1分)
---------------------------------------------------------------------(1分)
(3)若对任意-----理科数学.files/image187.gif) ,不等式
,不等式-----理科数学.files/image189.gif) 恒成立,
恒成立,
即:-----理科数学.files/image359.gif)
-----理科数学.files/image361.gif) -------------------------------------------(1分)
-------------------------------------------(1分)
令:-----理科数学.files/image363.gif) ,当
,当-----理科数学.files/image365.gif) 时,
时,-----理科数学.files/image367.gif) 有最大值为0---------------(1分)
有最大值为0---------------(1分)
令:-----理科数学.files/image369.gif)
-----理科数学.files/image371.gif) ------------------------------------------------------(1分)
------------------------------------------------------(1分)
当-----理科数学.files/image373.gif) 时
时
-----理科数学.files/image375.gif)
-----理科数学.files/image377.gif) ---------------------------------------------------------(1分)
---------------------------------------------------------(1分)
所以,数列-----理科数学.files/image379.gif) 从第二项起单调递减
从第二项起单调递减
当-----理科数学.files/image381.gif) 时,
时,-----理科数学.files/image383.gif) 取得最大值为1-------------------------------(1分)
取得最大值为1-------------------------------(1分)
所以,当-----理科数学.files/image385.gif) 时,不等式
时,不等式-----理科数学.files/image189.gif) 恒成立---------(1分)
恒成立---------(1分)
21. 解:
(1)双曲线-----理科数学.files/image191.gif) 焦点坐标为
焦点坐标为-----理科数学.files/image387.gif) ,渐近线方程
,渐近线方程-----理科数学.files/image389.gif) ---(2分)
---(2分)
双曲线-----理科数学.files/image195.gif) 焦点坐标
焦点坐标-----理科数学.files/image387.gif) ,渐近线方程
,渐近线方程-----理科数学.files/image392.gif) ----(2分)
----(2分)
(2)-----理科数学.files/image393.jpg)
得方程:-----理科数学.files/image395.gif) -------------------------------------------(1分)
-------------------------------------------(1分)
设直线分别与双曲线-----理科数学.files/image191.gif) 的交点
的交点-----理科数学.files/image397.gif) 、
、-----理科数学.files/image228.gif) 的坐标分别为
的坐标分别为-----理科数学.files/image400.gif)
-----理科数学.files/image402.gif) ,线段
,线段-----理科数学.files/image397.gif)
-----理科数学.files/image228.gif) 中点为
中点为-----理科数学.files/image113.gif) 坐标为
坐标为-----理科数学.files/image405.gif)
-----理科数学.files/image407.gif) ----------------------------------------------------------(1分)
----------------------------------------------------------(1分)
-----理科数学.files/image408.jpg)
得方程:-----理科数学.files/image410.gif) ----------------------------------------(1分)
----------------------------------------(1分)
设直线分别与双曲线-----理科数学.files/image195.gif) 的交点
的交点-----理科数学.files/image106.gif) 、
、-----理科数学.files/image133.gif) 的坐标分别为
的坐标分别为-----理科数学.files/image415.gif)
-----理科数学.files/image417.gif) ,线段
,线段-----理科数学.files/image106.gif)
-----理科数学.files/image133.gif) 中点为
中点为-----理科数学.files/image115.gif) 坐标为
坐标为-----理科数学.files/image420.gif)
-----理科数学.files/image422.gif) ---------------------------------------------------(1分)
---------------------------------------------------(1分)
由-----理科数学.files/image424.gif) ,-----------------------------------------------------------(1分)
,-----------------------------------------------------------(1分)
所以,线段-----理科数学.files/image201.gif) 与
与-----理科数学.files/image203.gif) 不相等------------------------------------(1分)
不相等------------------------------------(1分)
(3)
若直线-----理科数学.files/image011.gif) 斜率不存在,交点总个数为4;-------------------------(1分)
斜率不存在,交点总个数为4;-------------------------(1分)
若直线-----理科数学.files/image011.gif) 斜率存在,设斜率为
斜率存在,设斜率为-----理科数学.files/image162.gif) ,直线
,直线-----理科数学.files/image011.gif) 方程为
方程为-----理科数学.files/image427.gif)
直线-----理科数学.files/image011.gif) 与双曲线
与双曲线-----理科数学.files/image191.gif) :
:
-----理科数学.files/image428.jpg)
得方程:-----理科数学.files/image430.gif) ①
①
直线-----理科数学.files/image011.gif) 与双曲线
与双曲线-----理科数学.files/image195.gif) :
:
-----理科数学.files/image431.jpg)
得方程: -----理科数学.files/image433.gif) ②-----------(1分)
②-----------(1分)
-----理科数学.files/image162.gif) 的取值
的取值
直线-----理科数学.files/image011.gif) 与双曲线
与双曲线-----理科数学.files/image191.gif) 右支的交点个数
右支的交点个数
直线-----理科数学.files/image011.gif) 与双曲线
与双曲线-----理科数学.files/image195.gif) 右支的交点个数
右支的交点个数
交点总个数
-----理科数学.files/image435.gif)
1个(交点-----理科数学.files/image437.gif) )
)
1个(交点-----理科数学.files/image439.gif) )
)
2个
-----理科数学.files/image441.gif)
1个(-----理科数学.files/image443.gif) ,
,-----理科数学.files/image445.gif) )
)
1个(-----理科数学.files/image443.gif) ,
,-----理科数学.files/image447.gif) )
)
2个
-----理科数学.files/image449.gif)
1个(与渐进线平行)
1个(理由同上)
2个
-----理科数学.files/image451.gif)
2个(-----理科数学.files/image443.gif) ,方程①两根都大于2)
,方程①两根都大于2)
1个(理由同上)
3个
-----理科数学.files/image453.gif)
2个(理由同上)
1个(与渐进线平行)
3个
-----理科数学.files/image455.gif)
2个(理由同上)
2个(-----理科数学.files/image443.gif) ,方程②
,方程②
两根都大于1)
4个
得:-------------------------------------------------------------------(3分)
由双曲线的对称性可得:
-----理科数学.files/image162.gif) 的取值
的取值
交点总个数
-----理科数学.files/image457.gif)
2个
-----理科数学.files/image459.gif)
2个
-----理科数学.files/image461.gif)
3个
-----理科数学.files/image463.gif)
3个
-----理科数学.files/image465.gif)
4个
得:-------------------------------------------------------------------(2分)
综上所述:(1)若直线-----理科数学.files/image011.gif) 斜率不存在,交点总个数为4;
斜率不存在,交点总个数为4;
(2)若直线-----理科数学.files/image011.gif) 斜率存在,当
斜率存在,当-----理科数学.files/image467.gif) 时,交点总个数为2个;当
时,交点总个数为2个;当-----理科数学.files/image469.gif) 或
或-----理科数学.files/image471.gif) 时,交点总个数为3个;当
时,交点总个数为3个;当-----理科数学.files/image455.gif) 或
或-----理科数学.files/image465.gif) 时,交点总个数为4个;---------------(1分)
时,交点总个数为4个;---------------(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com