
题目列表(包括答案和解析)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
“![]() ”是“对任意的正数
”是“对任意的正数![]() ,
,![]() ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
“ ”是“对任意的正数
”是“对任意的正数 ,
, ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
“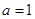 ”是“对任意的正数
”是“对任意的正数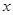 ,
,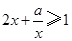 ”的()
”的()
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
“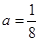 ”是“对任意的正数
”是“对任意的正数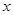 ,
,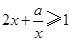 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
一、填空题
1.-----文科数学.files/image178.gif) 2.
2. -----文科数学.files/image180.gif) 3.2 4.
3.2 4.-----文科数学.files/image182.gif) 5. 10
6.i
5. 10
6.i-----文科数学.files/image184.gif) 100 7.
100 7. -----文科数学.files/image186.gif)
8. -----文科数学.files/image188.gif) 9.
9. -----文科数学.files/image190.gif) 10.
10. -----文科数学.files/image192.gif) 11.
11.-----文科数学.files/image194.gif) 12.
12.-----文科数学.files/image196.gif)
二、选择题
13. -----文科数学.files/image198.gif) 14.A 15.A. 16. D
14.A 15.A. 16. D
三、解答题
17.由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥V-ABCD ;-----------------------------------------(3分)
(1) -----文科数学.files/image200.gif) -------------(3分)
-------------(3分)
(2) 该四棱锥有两个侧面VAD. VBC是全等的等腰三角形,且BC边上的高为
-----文科数学.files/image202.gif) ,
---------------------(2分)
,
---------------------(2分)
另两个侧面VAB. VCD也是全等的等腰三角形,
AB边上的高为 -----文科数学.files/image204.gif) -------(2分)
-------(2分)
因此 -----文科数学.files/image206.gif) ------(2分)
------(2分)
18.
(1)由题意可得:-----文科数学.files/image104.gif) =5---------------------------(2分)
=5---------------------------(2分)
由:-----文科数学.files/image208.gif) 得:
得:-----文科数学.files/image109.gif) =314--------(4分)
=314--------(4分)
或:-----文科数学.files/image210.gif) ,
,-----文科数学.files/image212.gif)
(2)方法一:由:-----文科数学.files/image214.gif) 或
或-----文科数学.files/image216.gif) ------(1分)
------(1分)
-----文科数学.files/image218.gif) 或
或-----文科数学.files/image220.gif) --------(2分)
--------(2分)
得:-----文科数学.files/image222.gif) 0.0110-------------------------------------------------------------(1分)
0.0110-------------------------------------------------------------(1分)
方法二:由:-----文科数学.files/image224.gif)
得:-----文科数学.files/image226.gif) ----------------------------------------------------------------(1分)
----------------------------------------------------------------(1分)
由:-----文科数学.files/image111.gif) 点和
点和-----文科数学.files/image113.gif) 点的纵坐标相等,可得
点的纵坐标相等,可得-----文科数学.files/image111.gif) 点和
点和-----文科数学.files/image113.gif) 点关于
点关于-----文科数学.files/image125.gif) 点对称---(1分)
点对称---(1分)
即:-----文科数学.files/image231.gif) ------------------------------------------------------------(1分)
------------------------------------------------------------(1分)
得:-----文科数学.files/image222.gif) 0.011-----------------------------------------------------------------------(1分)
0.011-----------------------------------------------------------------------(1分)
(理科二种解法各1分)
19.解:(1)、函数-----文科数学.files/image133.gif) 的定义域为R;----------------------------(1分)
的定义域为R;----------------------------(1分)
当-----文科数学.files/image233.gif) 时
时-----文科数学.files/image235.gif) ;当
;当-----文科数学.files/image237.gif) 时
时-----文科数学.files/image239.gif) ;当
;当-----文科数学.files/image241.gif) 时
时-----文科数学.files/image243.gif) ;----------(1分)
;----------(1分)
所以,函数-----文科数学.files/image133.gif) 在定义域R上不是单调函数,----------------------(1分)
在定义域R上不是单调函数,----------------------(1分)
所以它不是“-----文科数学.files/image104.gif) 类函数” -----------------------------------------------------------(1分)
类函数” -----------------------------------------------------------(1分)
(2)函数-----文科数学.files/image245.gif) 在
在-----文科数学.files/image247.gif) 上单调递增,--------------------------(2分)
上单调递增,--------------------------(2分)
要使它是“-----文科数学.files/image104.gif) 类函数”,即存在两个不相等的常数
类函数”,即存在两个不相等的常数-----文科数学.files/image249.gif) ,
,-----文科数学.files/image251.gif)
使得-----文科数学.files/image253.gif) 同时
同时-----文科数学.files/image255.gif) 成立,------------------------(1分)
成立,------------------------(1分)
即关于-----文科数学.files/image084.gif) 的方程
的方程-----文科数学.files/image258.gif) 有两个不相等的实根,-------------------(2分)
有两个不相等的实根,-------------------(2分)
-----文科数学.files/image260.gif) ,--------------------------------------------------------------(1分)
,--------------------------------------------------------------(1分)
亦即直线-----文科数学.files/image262.gif) 与曲线
与曲线-----文科数学.files/image264.gif) 在
在-----文科数学.files/image247.gif) 上有两个不同的交点,-(2分)
上有两个不同的交点,-(2分)
所以,-----文科数学.files/image266.gif) ----------------------------------------------------------------------------(2分)
----------------------------------------------------------------------------(2分)
20.解:
(1)-----文科数学.files/image268.gif)
-----文科数学.files/image270.gif)
若-----文科数学.files/image272.gif) ,由
,由-----文科数学.files/image274.gif) ,得数列
,得数列-----文科数学.files/image147.gif) 构成等比数列------------------(3分)
构成等比数列------------------(3分)
若-----文科数学.files/image276.gif) ,
,-----文科数学.files/image278.gif) ,数列
,数列-----文科数学.files/image147.gif) 不构成等比数列--------------------------------------(1分)
不构成等比数列--------------------------------------(1分)
(2)由-----文科数学.files/image280.gif) ,得:
,得:-----文科数学.files/image282.gif) -------------------------------------(1分)
-------------------------------------(1分)
-----文科数学.files/image284.gif) ---------------------------------------------------------(1分)
---------------------------------------------------------(1分)
-----文科数学.files/image286.gif) ----------------------------------------------(1分)
----------------------------------------------(1分)
-----文科数学.files/image288.gif)
-----文科数学.files/image290.gif)
-----文科数学.files/image292.gif) ----(1分)
----(1分)
-----文科数学.files/image294.gif) ------------------------------------------------------------------(1分)
------------------------------------------------------------------(1分)
-----文科数学.files/image296.gif) ---------------------------------------------------------------------(1分)
---------------------------------------------------------------------(1分)
(3)
由:-----文科数学.files/image155.gif)
得:-----文科数学.files/image298.gif) ----------------------------------------------------(2分)
----------------------------------------------------(2分)
-----文科数学.files/image300.gif) ---------------------------------------------(1分)
---------------------------------------------(1分)
当-----文科数学.files/image302.gif) 时
时
-----文科数学.files/image304.gif)
-----文科数学.files/image306.gif)
所以,数列-----文科数学.files/image158.gif) 从第二项起单调递增数列----------------------(2分)
从第二项起单调递增数列----------------------(2分)
当-----文科数学.files/image309.gif) 时,
时,-----文科数学.files/image311.gif) 取得最小值为
取得最小值为-----文科数学.files/image313.gif) -------------------------(1分)
-------------------------(1分)
21. 解:
(1)双曲线-----文科数学.files/image160.gif) 焦点坐标为
焦点坐标为-----文科数学.files/image315.gif) ,渐近线方程
,渐近线方程-----文科数学.files/image317.gif) ---(2分)
---(2分)
双曲线-----文科数学.files/image164.gif) 焦点坐标
焦点坐标-----文科数学.files/image315.gif) ,渐近线方程
,渐近线方程-----文科数学.files/image320.gif) ----(2分)
----(2分)
(2)-----文科数学.files/image321.jpg)
得方程:-----文科数学.files/image323.gif) -------------------------------------------(1分)
-------------------------------------------(1分)
设直线分别与双曲线-----文科数学.files/image160.gif) 的交点
的交点-----文科数学.files/image325.gif) 、
、-----文科数学.files/image198.gif) 的坐标分别为
的坐标分别为-----文科数学.files/image328.gif)
-----文科数学.files/image330.gif) ,线段
,线段-----文科数学.files/image325.gif)
-----文科数学.files/image198.gif) 中点为
中点为-----文科数学.files/image111.gif) 坐标为
坐标为-----文科数学.files/image333.gif)
-----文科数学.files/image335.gif) ----------------------------------------------------------(1分)
----------------------------------------------------------(1分)
-----文科数学.files/image336.jpg)
得方程:-----文科数学.files/image338.gif) ----------------------------------------(1分)
----------------------------------------(1分)
设直线分别与双曲线-----文科数学.files/image164.gif) 的交点
的交点-----文科数学.files/image104.gif) 、
、-----文科数学.files/image125.gif) 的坐标分别为
的坐标分别为-----文科数学.files/image343.gif)
-----文科数学.files/image345.gif) ,线段
,线段-----文科数学.files/image104.gif)
-----文科数学.files/image125.gif) 中点为
中点为-----文科数学.files/image113.gif) 坐标为
坐标为-----文科数学.files/image348.gif)
-----文科数学.files/image350.gif) ---------------------------------------------------(1分)
---------------------------------------------------(1分)
由-----文科数学.files/image352.gif) ,-----------------------------------------------------------(1分)
,-----------------------------------------------------------(1分)
所以,线段-----文科数学.files/image170.gif) 与
与-----文科数学.files/image172.gif) 不相等------------------------------------(1分)
不相等------------------------------------(1分)
(3)
若直线-----文科数学.files/image174.gif) 斜率不存在,交点总个数为4;-------------------------(1分)
斜率不存在,交点总个数为4;-------------------------(1分)
若直线-----文科数学.files/image174.gif) 斜率存在,设斜率为
斜率存在,设斜率为-----文科数学.files/image031.gif) ,直线
,直线-----文科数学.files/image174.gif) 方程为
方程为-----文科数学.files/image355.gif)
直线-----文科数学.files/image174.gif) 与双曲线
与双曲线-----文科数学.files/image160.gif) :
:
-----文科数学.files/image356.jpg)
得方程:-----文科数学.files/image358.gif) ①
①
直线-----文科数学.files/image174.gif) 与双曲线
与双曲线-----文科数学.files/image164.gif) :
:
-----文科数学.files/image359.jpg)
得方程: -----文科数学.files/image361.gif) ②-----------(1分)
②-----------(1分)
-----文科数学.files/image031.gif) 的取值
的取值
直线-----文科数学.files/image174.gif) 与双曲线
与双曲线-----文科数学.files/image160.gif) 右支的交点个数
右支的交点个数
直线-----文科数学.files/image174.gif) 与双曲线
与双曲线-----文科数学.files/image164.gif) 右支的交点个数
右支的交点个数
交点总个数
-----文科数学.files/image363.gif)
1个(交点-----文科数学.files/image365.gif) )
)
1个(交点-----文科数学.files/image367.gif) )
)
2个
-----文科数学.files/image369.gif)
1个(-----文科数学.files/image371.gif) ,
,-----文科数学.files/image373.gif) )
)
1个(-----文科数学.files/image371.gif) ,
,-----文科数学.files/image375.gif) )
)
2个
-----文科数学.files/image377.gif)
1个(与渐进线平行)
1个(理由同上)
2个
-----文科数学.files/image379.gif)
2个(-----文科数学.files/image371.gif) ,方程①两根都大于2)
,方程①两根都大于2)
1个(理由同上)
3个
-----文科数学.files/image381.gif)
2个(理由同上)
1个(与渐进线平行)
3个
-----文科数学.files/image383.gif)
2个(理由同上)
2个(-----文科数学.files/image371.gif) ,方程②
,方程②
两根都大于1)
4个
得:-------------------------------------------------------------------(3分)
由双曲线的对称性可得:
-----文科数学.files/image031.gif) 的取值
的取值
交点总个数
-----文科数学.files/image385.gif)
2个
-----文科数学.files/image387.gif)
2个
-----文科数学.files/image389.gif)
3个
-----文科数学.files/image391.gif)
3个
-----文科数学.files/image393.gif)
4个
得:-------------------------------------------------------------------(2分)
综上所述:(1)若直线-----文科数学.files/image174.gif) 斜率不存在,交点总个数为4;
斜率不存在,交点总个数为4;
(2)若直线-----文科数学.files/image174.gif) 斜率存在,当
斜率存在,当-----文科数学.files/image395.gif) 时,交点总个数为2个;当
时,交点总个数为2个;当-----文科数学.files/image397.gif) 或
或-----文科数学.files/image399.gif) 时,交点总个数为3个;当
时,交点总个数为3个;当-----文科数学.files/image383.gif) 或
或-----文科数学.files/image393.gif) 时,交点总个数为4个;---------------(1分)
时,交点总个数为4个;---------------(1分)
上海市奉贤区2009年4月高考模拟考试
数学试题(文)
考生注意:
1.答卷前,考生务必在答题纸上将姓名、高考准考证号填写清楚,并在规定的区域内贴上条形码.
2.本试卷共有21道试题,满分150分.考试时间120分钟.
-----文科数学.files/image001.gif) 一、填空题(本大题满分60分)本大题共有12题,只要求在答题纸相应题序的空格内直接填写结果,每个空格填对得5分,否则一律得零分.
一、填空题(本大题满分60分)本大题共有12题,只要求在答题纸相应题序的空格内直接填写结果,每个空格填对得5分,否则一律得零分.
1.-----文科数学.files/image003.gif) ___________.
___________.
2.函数-----文科数学.files/image005.gif) 的定义域为__________ .
的定义域为__________ .
3.已知复数-----文科数学.files/image007.gif) ,则
,则-----文科数学.files/image009.gif) ____________.
____________.
4.-----文科数学.files/image011.gif) 的值为
的值为
5.-----文科数学.files/image013.gif) 的展开式中
的展开式中-----文科数学.files/image015.gif) 的系数为
.
的系数为
.
6.右图给出的是计算-----文科数学.files/image017.gif) 的值的一个程序框图,
的值的一个程序框图,
其中判断框内应填入的条件是__________.
7.计算:设向量-----文科数学.files/image019.gif) ,若向量
,若向量-----文科数学.files/image021.gif) 与向量
与向量-----文科数学.files/image023.gif) 垂直,则实数
垂直,则实数-----文科数学.files/image025.gif) .
.
8.若直线-----文科数学.files/image027.gif) 与圆
与圆-----文科数学.files/image029.gif) 没有公共点,则实数
没有公共点,则实数-----文科数学.files/image031.gif) 的取值范围是___________.
的取值范围是___________.
9.在等差数列-----文科数学.files/image033.gif) 中,设
中,设-----文科数学.files/image035.gif) ,对任意
,对任意-----文科数学.files/image037.gif) ,有
,有-----文科数学.files/image039.gif) 则
则-----文科数学.files/image041.gif) _____________.
_____________.
|