
题目列表(包括答案和解析)
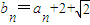 ,问数列{bn}中是否存在不同的3项,使之成为等比数列?若存在,试写出任意符合条件的3项;若不存在,请说明理由.
,问数列{bn}中是否存在不同的3项,使之成为等比数列?若存在,试写出任意符合条件的3项;若不存在,请说明理由.| 2 |
(本小题满分13分)已知数列{an}的前n项和为Sn,满足关系式(2+t)Sn+1-tSn=2t+4(t≠-2,t≠0,n=1,2,3,…)
(1)当a1为何值时,数列{an}是等比数列;
(2)在(1)的条件下,设数列{an}的公比为f(t),作数列{bn}使b1=1,bn=f(bn-1)(n=2,
3,4,…),求bn;
(3)在(2)条件下,如果对一切n∈N+,不等式bn+bn+1<恒成立,求实数c的取值范围.
(本小题满分13分)已知数列{an}的前n项和为Sn,满足关系式(2+t)Sn+1-tSn=2t+4(t≠-2,t≠0,n=1,2,3,…)
(1)当a1为何值时,数列{an}是等比数列;
(2)在(1)的条件下,设数列{an}的公比为f(t),作数列{bn}使b1=1,bn=f(bn-1)(n=2,
3,4,…),求bn;
(3)在(2)条件下,如果对一切n∈N+,不等式bn+bn+1<恒成立,求实数c的取值范围.
(本小题满分13分)已知数列{an}的前n项和为Sn,满足关系式(2+t)Sn+1-tSn=2t+4(t≠-2,t≠0,n=1,2,3,…)
(1)当a1为何值时,数列{an}是等比数列;
(2)在(1)的条件下,设数列{an}的公比为f(t),作数列{bn}使b1=1,bn=f(bn-1)(n=2,
3,4,…),求bn;
(3)在(2)条件下,如果对一切n∈N+,不等式bn+bn+1<恒成立,求实数c的取值范围.
第Ⅰ卷
一、选择题
题号
1
2
3
4
5
6
7
8
答案
B
B
B
A
C
A
D
C
第Ⅱ卷
二、填空题
9、3 , 高考模拟题.files/image196.gif) ; 10、
; 10、高考模拟题.files/image198.gif) ;
11、(A)
;
11、(A)高考模拟题.files/image200.gif) ; (B)
; (B)高考模拟题.files/image202.gif) ;(C)
;(C)高考模拟题.files/image204.gif) (
(高考模拟题.files/image206.gif) ); 12、0.5 13、28 ,
); 12、0.5 13、28 , 高考模拟题.files/image208.gif)
三、解答题
14、(本小题满分12分)
解:(Ⅰ)高考模拟题.files/image133.gif) =
=高考模拟题.files/image127.gif)
高考模拟题.files/image212.gif)
高考模拟题.files/image131.gif)
=高考模拟题.files/image214.gif) +
+高考模拟题.files/image216.gif)
=高考模拟题.files/image218.gif) +
+高考模拟题.files/image216.gif)
高考模拟题.files/image220.gif)
所以,高考模拟题.files/image135.gif) 的最小正周期
的最小正周期 高考模拟题.files/image223.gif)
高考模拟题.files/image225.gif)
(Ⅱ)高考模拟题.files/image227.gif)
高考模拟题.files/image139.gif)
高考模拟题.files/image230.gif)
高考模拟题.files/image232.gif)
高考模拟题.files/image234.gif)
高考模拟题.files/image230.gif)
高考模拟题.files/image237.gif)
由三角函数图象知:
高考模拟题.files/image239.gif)
高考模拟题.files/image241.gif) 的取值范围是
的取值范围是高考模拟题.files/image243.gif)
高考模拟题.files/image244.gif) 15、(本小题满分12分)
15、(本小题满分12分)
方法一:
证:(Ⅰ)在Rt△BAD中,AD=2,BD=高考模拟题.files/image143.gif) ,
,
∴AB=2,ABCD为正方形,
因此BD⊥AC.
∵PA⊥平面ABCD,BDÌ平面ABCD,
∴BD⊥PA .
又∵PA∩AC=A
∴BD⊥平面PAC.
解:(Ⅱ)由PA⊥面ABCD,知AD为PD在平面ABCD的射影,又CD⊥AD,
∴CD⊥PD,知∠PDA为二面角P―CD―B的平面角.
又∵PA=AD,
∴∠PDA=450 .
(Ⅲ)∵PA=AB=AD=2
∴PB=PD=BD=高考模拟题.files/image143.gif)
设C到面PBD的距离为d,由高考模拟题.files/image248.gif) ,
,
有高考模拟题.files/image250.gif) ,
,
高考模拟题.files/image251.gif) 即
即高考模拟题.files/image253.gif) ,
,
得高考模拟题.files/image255.gif)
方法二:
证:(Ⅰ)建立如图所示的直角坐标系,
则A(0,0,0)、D(0,2,0)、P(0,0,2).
在Rt△BAD中,AD=2,BD=高考模拟题.files/image143.gif) ,
,
∴AB=2.
∴B(2,0,0)、C(2,2,0),
∴高考模拟题.files/image257.gif)
∵高考模拟题.files/image259.gif)
即BD⊥AP,BD⊥AC,又AP∩AC=A,
∴BD⊥平面PAC.
解:(Ⅱ)由(Ⅰ)得高考模拟题.files/image261.gif) .
.
设平面PCD的法向量为高考模拟题.files/image263.gif) ,则
,则高考模拟题.files/image265.gif) ,
,
即高考模拟题.files/image267.gif) ,∴
,∴高考模拟题.files/image269.gif)
故平面PCD的法向量可取为高考模拟题.files/image271.gif)
∵PA⊥平面ABCD,∴高考模拟题.files/image273.gif) 为平面ABCD的法向量.
为平面ABCD的法向量.
设二面角P―CD―B的大小为q,依题意可得高考模拟题.files/image275.gif) ,
,
∴q = 450 .
(Ⅲ)由(Ⅰ)得高考模拟题.files/image277.gif)
设平面PBD的法向量为高考模拟题.files/image279.gif) ,则
,则高考模拟题.files/image281.gif) ,
,
即高考模拟题.files/image283.gif) ,∴x=y=z
,∴x=y=z
故平面PBD的法向量可取为高考模拟题.files/image285.gif) .
.
∵高考模拟题.files/image287.gif) ,
,
∴C到面PBD的距离为高考模拟题.files/image289.gif)
16、(本小题满分14分)
解:(1)设“甲射击4次,至少1次未击中目标”为事件A,则其对立事件高考模拟题.files/image291.gif) 为“4次均击中目标”,则
为“4次均击中目标”,则高考模拟题.files/image293.gif)
(2)设“甲恰好击中目标2次且乙恰好击中目标3次”为事件B,则
高考模拟题.files/image295.gif)
(3)设“乙恰好射击5次后,被中止射击”为事件C,由于乙恰好射击5次后被中止射击,故必然是最后两次未击中目标,第三次击中目标,第一次及第二次至多有一次未击中目标。
故高考模拟题.files/image297.gif)
17、(本小题满分14分)
解:(Ⅰ)由
高考模拟题.files/image299.gif) 得
得 高考模拟题.files/image301.gif)
即高考模拟题.files/image303.gif)
可得高考模拟题.files/image305.gif)
因为高考模拟题.files/image307.gif) ,所以
,所以 高考模拟题.files/image309.gif) 解得
解得高考模拟题.files/image311.gif) ,因而
,因而 高考模拟题.files/image313.gif)
(Ⅱ)因为高考模拟题.files/image315.gif) 是首项
是首项高考模拟题.files/image317.gif) 、公比
、公比高考模拟题.files/image311.gif) 的等比数列,故
的等比数列,故
高考模拟题.files/image320.gif)
则数列高考模拟题.files/image322.gif) 的前n项和
的前n项和 高考模拟题.files/image324.gif)
高考模拟题.files/image326.gif)
前两式相减,得 高考模拟题.files/image328.gif)
高考模拟题.files/image330.gif) 即
即 高考模拟题.files/image332.gif)
18、(本小题满分14分)
解:(1) 高考模拟题.files/image334.gif) ,设切点为
,设切点为高考模拟题.files/image336.gif) ,则曲线
,则曲线高考模拟题.files/image338.gif) 在点P的切线的斜率
在点P的切线的斜率高考模拟题.files/image340.gif) ,由题意知
,由题意知高考模拟题.files/image342.gif) 有解,
有解,
∴高考模拟题.files/image344.gif) 即
即高考模拟题.files/image346.gif) .
.
(2)若函数高考模拟题.files/image164.gif) 可以在
可以在高考模拟题.files/image166.gif) 和
和高考模拟题.files/image168.gif) 时取得极值,
时取得极值,
则高考模拟题.files/image348.gif) 有两个解
有两个解高考模拟题.files/image166.gif) 和
和高考模拟题.files/image168.gif) ,且满足
,且满足高考模拟题.files/image346.gif) .
.
易得高考模拟题.files/image350.gif) .
.
(3)由(2),得高考模拟题.files/image352.gif) .
.
根据题意,高考模拟题.files/image354.gif) (
(高考模拟题.files/image172.gif) )恒成立.
)恒成立.
∵函数高考模拟题.files/image356.gif) (
(高考模拟题.files/image172.gif) )在
)在高考模拟题.files/image166.gif) 时有极大值
时有极大值高考模拟题.files/image359.gif) (用求导的方法),
(用求导的方法),
且在端点高考模拟题.files/image361.gif) 处的值为
处的值为高考模拟题.files/image363.gif) .
.
∴函数高考模拟题.files/image356.gif) (
(高考模拟题.files/image172.gif) )的最大值为
)的最大值为高考模拟题.files/image363.gif) .
.
所以高考模拟题.files/image365.gif) .
.
19、(本小题满分14分)
解:(1)∵高考模拟题.files/image367.gif) 成等比数列 ∴
成等比数列 ∴高考模拟题.files/image369.gif)
高考模拟题.files/image371.gif)
设高考模拟题.files/image373.gif) 是椭圆上任意一点,依椭圆的定义得
是椭圆上任意一点,依椭圆的定义得
高考模拟题.files/image375.gif)
即高考模拟题.files/image377.gif) 为所求的椭圆方程.
为所求的椭圆方程.
(2)假设高考模拟题.files/image185.gif) 存在,因
存在,因高考模拟题.files/image185.gif) 与直线
与直线高考模拟题.files/image380.gif) 相交,不可能垂直
相交,不可能垂直高考模拟题.files/image141.gif) 轴
轴
因此可设高考模拟题.files/image185.gif) 的方程为:
的方程为:高考模拟题.files/image383.gif) 由
由
高考模拟题.files/image385.gif)
高考模拟题.files/image387.gif) ①
①
方程①有两个不等的实数根
∴高考模拟题.files/image389.gif) ②
②
设两个交点高考模拟题.files/image187.gif) 、
、高考模拟题.files/image189.gif) 的坐标分别为
的坐标分别为高考模拟题.files/image393.gif) ∴
∴高考模拟题.files/image395.gif)
∵线段高考模拟题.files/image191.gif) 恰被直线
恰被直线高考模拟题.files/image380.gif) 平分 ∴
平分 ∴高考模拟题.files/image399.gif)
∵高考模拟题.files/image401.gif) ∴
∴高考模拟题.files/image403.gif) ③ 把③代入②得
③ 把③代入②得 高考模拟题.files/image405.gif)
∵高考模拟题.files/image407.gif) ∴
∴高考模拟题.files/image409.gif) ∴
∴高考模拟题.files/image411.gif) 解得
解得高考模拟题.files/image413.gif) 或
或高考模拟题.files/image415.gif)
∴直线高考模拟题.files/image185.gif) 的倾斜角范围为
的倾斜角范围为高考模拟题.files/image418.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com