
当n≥6时,不存在这样的等差数列。事实上,在数列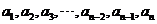 中,由于不能删去首项或末项,若删去
中,由于不能删去首项或末项,若删去 ,则必有
,则必有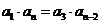 ,这与
,这与 矛盾;同样若删去
矛盾;同样若删去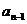 也有
也有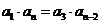 ,这与
,这与 矛盾;若删去
矛盾;若删去 中任意一个,则必有
中任意一个,则必有 ,这与
,这与 矛盾。(或者说:当n≥6时,无论删去哪一项,剩余的项中必有连续的三项)
矛盾。(或者说:当n≥6时,无论删去哪一项,剩余的项中必有连续的三项)
若删去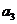 ,则
,则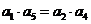 ,即
,即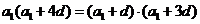 化简得
化简得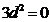 ,因为
,因为 ,所以
,所以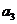 不能删去;
不能删去;
②当n=5时,  中同样不可能删去
中同样不可能删去 ,否则出现连续三项。
,否则出现连续三项。
综上,得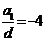 或
或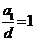 。
。
若删去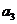 ,则
,则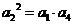 ,即
,即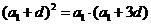 化简得
化简得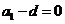 ,得
,得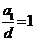
若删去 ,则
,则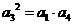 ,即
,即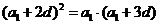 化简得
化简得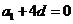 ,得
,得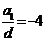
解:(1)①当n=4时, 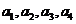 中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。
中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。
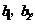
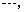
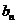 ,其中任意三项(按原来的顺序)都不能组成等比数列.
,其中任意三项(按原来的顺序)都不能组成等比数列.
(2)求证:对于给定的正整数 (
(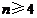 ),存在一个各项及公差均不为零的等差数列
),存在一个各项及公差均不为零的等差数列
(ii)求 的所有可能值.
的所有可能值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com