
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
解:(Ⅰ)设“甲投球一次命中”为事件A,“乙投球一次命中”为事件B
(Ⅰ)求乙投球的命中率 ;
;
46.甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为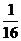 .
.
解:古典概型问题,基本事件总数为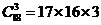 。能组成以3为公差的等差数列有(1,4,7),(2,5,8),
。能组成以3为公差的等差数列有(1,4,7),(2,5,8),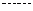 ,(12,15,18)共12组,因此概率
,(12,15,18)共12组,因此概率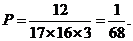
45.在某地的奥运火炬传递活动中,有编号为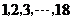 的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为
的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为
所以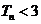 .
.
概率、统计(随机事件与概率A;古典概型B;几何概型A;互斥事件及其发生的概率A;统计案例A)
又因为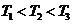 ,
,
故当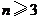 时,
时,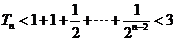 ,
,
于是 ,
,
所以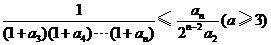 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com