
(2)若在椭圆C上存在点Q,满足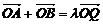 (O为坐标原点),求实数λ的取值范围.
(O为坐标原点),求实数λ的取值范围.
已知椭圆C的中心在原点,焦点在x轴上,点F1、F2分别是椭圆的左、右焦点,在直线x=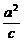 (a、c分别为椭圆的长半轴和半焦距的长)上的点P(2,
(a、c分别为椭圆的长半轴和半焦距的长)上的点P(2, 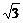 ),满足线段PF1的中垂线过点F2,直线l:y=kx+m为动直线,且直线l与椭圆C交于不同的两点A、B.
),满足线段PF1的中垂线过点F2,直线l:y=kx+m为动直线,且直线l与椭圆C交于不同的两点A、B.
(1)求椭圆C的方程;
21.(本小题满分12分)
20.(本小题满分12分)
已知数列{an}满足an+1=2an+n+1(n=1,2,3,……).
(1)若a1=-1,求证数列{an+n+2}为等比数列,并求{an}的前n项和Sn.
(2)求证{an}不可能是等比数列;
 19.(本小题满分12分)
19.(本小题满分12分)
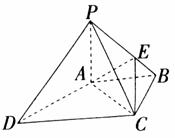
如图,四棱锥P―ABCD中,PA⊥底面ABCD,PC⊥AD。底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求平面AEC和平面PBC所成锐二面角的余弦值。
在一次抗洪抢险中,准备用射击的方法引爆从上游漂流而下的一巨大汽油罐。已知只有5发子弹,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中概率都是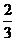 ,且每次命中与否互相独立.
,且每次命中与否互相独立.
(1)求油罐被引爆的概率;
(2)如果油罐引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望。
18.(本小题满分12分)
(2)若f (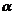 )=
)= 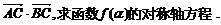
(1)若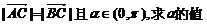 ;
;
已知点A (2,0), B (0,2), C (cos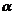 , sin
, sin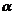 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com