1．在复平面内复数对应的点位于

C．实轴上                              D．虚轴上

       已知函数f (x)=

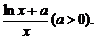
       （1）求f(x)的极大值；

       （2）若函数f (x)的图象与函数g(x)=1的图象在区间(0，e²]上有公共点，求实数a的取值范围

寿光市2009年高考适应性训练试题

22.（本小题满分14分）

（2）在x轴上是否存在点M，使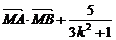是与k无关的常数？若存在，求出点M的坐标；若不存在，请说明理由。

（1）若线段AB中点的横坐标是-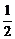，求直线AB的方程；

21.（本小题满分12分）

已知定点C(-1,0)及椭圆x²+3y²=5，过点C且斜率为k的直线与椭圆相交于不同的两点A，B.

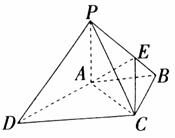       如图，四棱锥P―ABCD中，PA⊥底面ABCD，PC⊥AD。底面ABCD为梯形，AB∥DC，AB⊥BC，PA=AB=BC=1，点E在棱PB上，且PE=2EB.

       （1）求证：平面PAB⊥平面PCB；

       （2）求四棱锥P―ABCD的体积V；

       （3）求证：PD∥平面EAC.

       （注：棱锥体积=底面积×高÷3）

20.（本小题满分12分）

19.（本小题满分12分）

数列{a_n}中，a₁=-27，a_n+1+a_n=3n-54,（n∈N^*）.

（1）求证a₁, a₃, a₅, …和a₂, a₄, a₆，…分别成等差数列，并求数列{a_n}的通项公式；

（2）求数列{a_n}的前n（n为偶数）项和S_n的最小值.

18.（本小题满分12分）

       一个盒中放有除颜色不同外，其余完全相同的黑球和白球，其中黑球2个，白球3个；

       （1）从盒中同时摸出两个球，求两球颜色恰好相同的概率；

       （2）从盒中摸出一个球，放回后再摸出一个球，求两球颜色恰好不同的概率.