
(Ⅱ)是否存在直线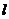 ,使得以线段
,使得以线段 为直径的圆过原点,若存在,求出直线
为直径的圆过原点,若存在,求出直线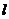 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(Ⅲ)若AB是椭圆C经过原点O的弦,MN∥AB,
求证:为定值.
(Ⅰ)求椭圆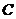 的方程;
的方程;
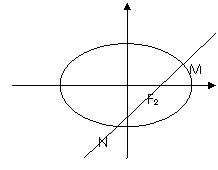 21.设椭圆
21.设椭圆 的一个顶点与抛物线
的一个顶点与抛物线 的焦点重合,
的焦点重合, ,
,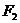 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率 =,过椭圆右焦点
=,过椭圆右焦点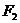 的直线
的直线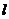 与椭圆
与椭圆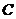 交于
交于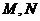 两点.
两点.
(Ⅲ)在(Ⅱ)的条件下,若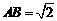 ,求二面角
,求二面角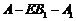 的平面角的正切值.
的平面角的正切值.
使得 (要求说明理由).
(要求说明理由).
(Ⅱ)试在棱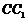 (不包含端点
(不包含端点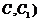 上确定一点
上确定一点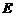 的位置,
的位置,
(Ⅰ)求证: ;
;
(Ⅲ)设 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望.
的分布列和数学期望.
19.已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com