
可看作是关于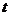 的一元二次方程
的一元二次方程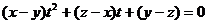 有等根的条件,在进一步观察这个方程,它的两个相等实根是1 ,根据韦达定理就有:
有等根的条件,在进一步观察这个方程,它的两个相等实根是1 ,根据韦达定理就有:
证明 当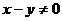 时,等式
时,等式 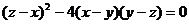
例5
若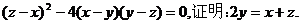
思路分析 此题一般是通过因式分解来证。但是,如果注意观察已知条件的特点,不难发现它与一元二次方程的判别式相似。于是,我们联想到借助一元二次方程的知识来证题。
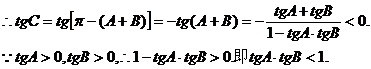
故应选择(B)
思维障碍 有的学生可能觉得此题条件太少,难以下手,原因是对三角函数的基本公式掌握得不牢固,不能准确把握公式的特征,因而不能很快联想到运用基本公式。
且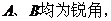
解 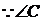 为钝角,
为钝角,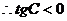 .在
.在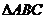 中
中
思路分析 此题是在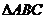 中确定三角函数
中确定三角函数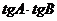 的值。因此,联想到三角函数正切的两角和公式
的值。因此,联想到三角函数正切的两角和公式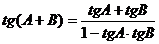 可得下面解法。
可得下面解法。
例4
在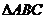 中,若
中,若
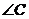 为钝角,则
为钝角,则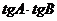 的值
的值
(A) 等于1 (B)小于1 (C) 大于1 (D) 不能确定
思维障碍 有些同学对比较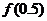 与
与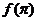 的大小,只想到求出它们的值。而此题函数
的大小,只想到求出它们的值。而此题函数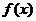 的表达式不确定无法代值,所以无法比较。出现这种情况的原因,是没有充分挖掘已知条件的含义,因而思维受到阻碍,做题时要全面看问题,对每一个已知条件都要仔细推敲,找出它的真正含义,这样才能顺利解题。提高思维的变通性。
的表达式不确定无法代值,所以无法比较。出现这种情况的原因,是没有充分挖掘已知条件的含义,因而思维受到阻碍,做题时要全面看问题,对每一个已知条件都要仔细推敲,找出它的真正含义,这样才能顺利解题。提高思维的变通性。
(2) 联想能力的训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com