
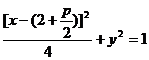 (2)
(2)
是,又从已知条件可得椭圆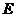 的方程为
的方程为
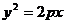 (1)
(1)
例12
直线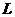 的方程为
的方程为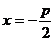 ,其中
,其中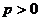 ;椭圆
;椭圆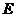 的中心为
的中心为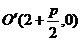 ,焦点在
,焦点在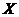 轴上,长半轴为2,短半轴为1,它的一个顶点为
轴上,长半轴为2,短半轴为1,它的一个顶点为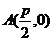 ,问
,问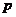 在什么范围内取值时,椭圆上有四个不同的点,它们中的每一点到点
在什么范围内取值时,椭圆上有四个不同的点,它们中的每一点到点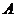 的距离等于该点到直线
的距离等于该点到直线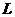 的距离。
的距离。
思路分析 从题目的要求及解析几何的知识可知,四个不同的点应在抛物线
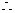
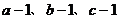 中至少有一个为零,即
中至少有一个为零,即 、
、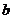 、
、 中至少有一个为1。
中至少有一个为1。
思维障碍 很多学生只在已知条件上下功夫,左变右变,还是不知如何证明三者中至少有一个为1,其原因是不能把要证的结论“翻译”成数学式子,把陌生问题变为熟悉问题。因此,多练习这种“翻译”,是提高转化能力的一种有效手段。
于是 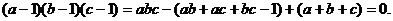
证明 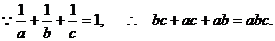
思路分析 结论没有用数学式子表示,很难直接证明。首先将结论用数学式子表示,转化成我们熟悉的形式。 、
、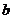 、
、 中至少有一个为1,也就是说
中至少有一个为1,也就是说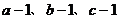 中至少有一个为零,这样,问题就容易解决了。
中至少有一个为零,这样,问题就容易解决了。
例11 已知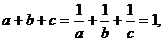 求证
求证 、
、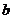 、
、 中至少有一个等于1。
中至少有一个等于1。
思维阻碍 由于这是一个关于自然数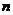 的命题,一些学生都会想到用数学归纳法来证明,难以进行数与形的联想,原因是平时不注意代数与几何之间的联系,单纯学代数,学几何,因而不能将题目条件的数字或式子特征与直观图形联想起来。
的命题,一些学生都会想到用数学归纳法来证明,难以进行数与形的联想,原因是平时不注意代数与几何之间的联系,单纯学代数,学几何,因而不能将题目条件的数字或式子特征与直观图形联想起来。
(3) 问题转化的训练
我们所遇见的数学题大都是生疏的、复杂的。在解题时,不仅要先观察具体特征,联想有关知识,而且要将其转化成我们比较熟悉的,简单的问题来解。恰当的转化,往往使问题很快得到解决,所以,进行问题转化的训练是很必要的。
1 转化成容易解决的明显题目
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com