与②矛盾，所以假设不成立，即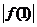、、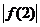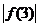中至少有一个不小于1。

    3  一题多解训练

    由于每个学生在观察时抓住问题的特点不同、运用的知识不同，因而，同一问题可能得到几种不同的解法，这就是“一题多解”。通过一题多解训练，可使学生认真观察、多方联想、恰当转化，提高数学思维的变通性。

①＋③得         ，

则              

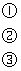
证明  （反证法）假设原命题不成立，即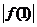、、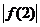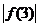都小于1。

例13  已知函数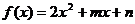，求证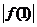、、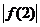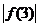中至少有一个不小于1.

思路分析  反证法被誉为“数学家最精良的武器之一”，它也是中学数学常用的解题方法。当要证结论中有“至少”等字样，或以否定形式给出时，一般可考虑采用反证法。

在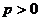的条件下，得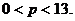

    本题在解题过程中，不断地把问题化归为标准问题：解方程组和不等式组的问题。

2  逆向思维的训练

逆向思维不是按习惯思维方向进行思考，而是从其反方向进行思考的一种思维方式。当问题的正面考虑有阻碍时，应考虑问题的反面，从反面入手，使问题得到解决。

确定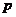的范围，实际上就是求（3）有两个不等正根的充要条件，解不等式组：

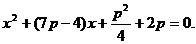                                         （3）

因此，问题转化为当方程组（1）、（2）有四个不同的实数解时，求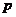的取值范围。将（2）代入（1）得：