
例10 求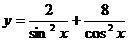 的最小值
的最小值
于是所求椭圆的方程为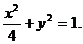
所以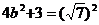 ,解得
,解得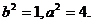
所以必有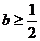 ,此时当
,此时当 时,
时,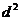 (从而
(从而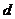 )有最大值,
)有最大值,
于是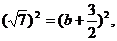 从而解得
从而解得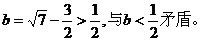
若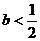 ,则当
,则当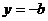 时,
时,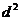 (从而
(从而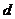 )有最大值。
)有最大值。
错解分析 尽管上面解法的最后结果是正确的,但这种解法却是错误的。结果正确只是碰巧而已。由当 时,
时,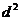 有最大值,这步推理是错误的,没有考虑
有最大值,这步推理是错误的,没有考虑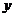 到的取值范围。事实上,由于点
到的取值范围。事实上,由于点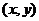 在椭圆上,所以有
在椭圆上,所以有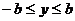 ,因此在求
,因此在求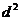 的最大值时,应分类讨论。即:
的最大值时,应分类讨论。即:
于是所求椭圆的方程为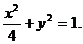
所以 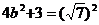 ,由此解得:
,由此解得: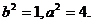
所以当 时,
时,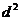 有最大值,从而
有最大值,从而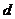 也有最大值。
也有最大值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com