16．（8分）如图10所示为宇宙中某一个恒星系的示意图，A为该星系的一颗行星，它绕中

                                   央恒星O运行，轨道近似为圆，天文学家观测得到A行星运动的轨道半径为R₀，周期为T₀，引力常量为G。

   （1）中央恒星O的质量是多大？

   （2）长期观测发现，A行星实际运动的轨道与圆轨道总存在一些偏离，且周期性地每隔

                                   t₀时间发生一次最大的偏离，天文学家认为形成这种现象的原因可能是A行星外侧

                                   还存在着一颗未知的行星B（假设其运动轨道与A在同一平面内，且与A的绕行方

   （3）若该小汽车发动机的额定率为25kw，汽车从静止开始，保持以0.6m/s²的加速度做

        匀速直线运动，这一过程能持续多长时间？

15．（8分）一辆微型小汽车在平直的高速公路上行驶，所受到的阻力大小恒定，若发动机的

    牵引力大小分别为F₁=50N和F₂=1550N时，小汽车运动的加速度大小均为a=1m/s²。则：

   （1）发动机的牵引力分别为F₁和F₂时，小汽车分别做什么运动？

   （2）求出小汽车的质量和其运动过程中所受到的阻力大小。

    然后再减速到v₂=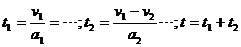20m/s，。

    你认为这位同学的解法是否合理？若合理，请完成计算；若不合理，请说明理由，并用

    你自己的方法算出正确结果。

14．（8分）要求摩托车由静止开始在尽量短的时间内走完一段直道，然后驶入一段半圆形的

    弯道，但在弯道上行驶时车速不能太快，以免因离心作用而偏出车道。求摩托车在直道

    上行驶所用的最短时间。有关数据见表格。               

    某同学是这样解的：要使摩托车所用时间最短，应先由静止加速到最大速度v₁=40m/s，

   ③若测得脱离动力时砂轮的角速度为2.5rad/s，则它转过45圈时的角速度为____rad/s。

启动加速度a₁

4m/s²

制动加速度a₂

8m/s²

直道最大速度v₁

40m/s

弯道最大速度v₂

20m/s

直道长度s

218m

5.0

20

80

180

320

500

E_K/J

  ①计算出砂轮每次脱离动力时的转动动能，并真入上表中。

   ②由上述数据推导出该砂轮的转动动能E_K与角速度ω的关系式为_________。

0.5

1

2

3

4

5

n