
6.下列根式中属最简二次根式的是( )
A.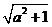 B.
B.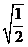 C.
C.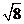 D.
D. 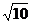
5. 下列命题中正确的是( )
A.对角线互相平分的四边形是菱形 B.对角线互相平分且相等的四边形是菱形
C.对角线互相垂直的四边形是菱形 D.对角线互相垂直平分的四边形是菱形
4. 已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C.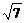 D.5或
D.5或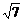
3.下列函数(1)y=3πx (2)y=8x-6 (3)y= (4)y=-8x (5)y=5x2-4x+1中,是一次函数的有( )
A.4个 B.3个 C.2个 D.1个
2. 下列条件之一能使平行四边形ABCD是菱形的为( )
①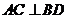 ②
②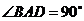 ③
③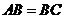 ④
④
A.①③ B.②③ C.③④ D.①②③
一、选择题
1. 如果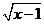 有意义,那么
有意义,那么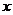 的取值范围是( )
的取值范围是( )
A.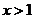 B.
B.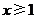 C.
C.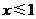 D.
D.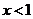
22.(本小题满分13份)
解:(I)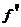
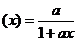
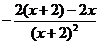 =
=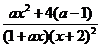
当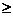 1时,
1时, ,此时
,此时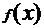 在区间
在区间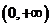 上单调递增。
上单调递增。
当0<a<1时,由 <0得
<0得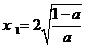 (
(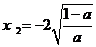 舍去)
舍去)
当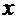 ∈(0,
∈(0,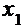 )时
)时 <0;当x∈
<0;当x∈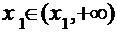 时,
时, >0
>0
故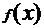 在区间(0,
在区间(0,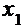 )上单调递增,在区间(
)上单调递增,在区间(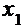 ,
,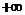 )上单调递增。
)上单调递增。
综上所述
当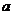
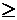
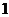 时,
时,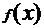 在区间(0,
在区间(0,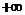 )上单调递增;
)上单调递增;
当0<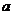 <1时,
<1时,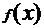 在区间(0,
在区间(0,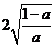 )上单调递减,在区间(
)上单调递减,在区间(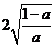 ,
,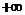 )上单调递增
)上单调递增
(II)由()式知。当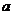
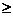
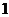 ,
,
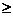 0,此时
0,此时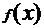 不存在极值点,因而要使得
不存在极值点,因而要使得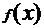 有两个极值点,必有0<
有两个极值点,必有0<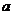 <1。又
<1。又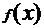 的极值点只可能是
的极值点只可能是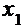 =
=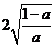 和
和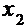 = -
= -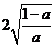 ,且由
,且由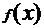 的定义可知,
的定义可知,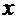 >
>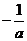 且
且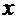
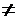 —2,所以
—2,所以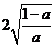 >
>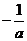 。
。
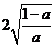
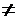 —2,解得
—2,解得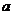
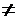
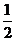 。此时,由()式易知,
。此时,由()式易知,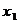 ,
,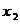 分别是
分别是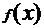 的极小值点和极大值点,而
的极小值点和极大值点,而
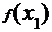 +
+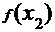 =
=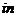 (
(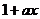 )-
)-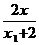 +
+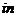 (1+
(1+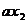 )-
)-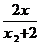
=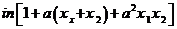 -
-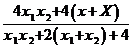
=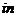
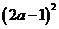 —
—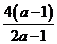 =
=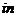
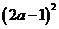 +
+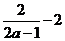
令2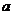 -1=x,由0<
-1=x,由0<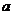 <1且
<1且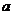
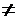
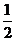 知
知
当0<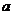 <
<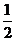 时,-1<x<0; 当
时,-1<x<0; 当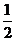 <
<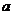 <1时。0<x<1
<1时。0<x<1
记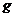 (x)=in
(x)=in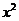 +
+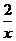 -2
-2
(i)
当-1<x<0时,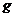 (x)=2in(-x)+
(x)=2in(-x)+ 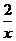 -2,所以
-2,所以
 (x)=
(x)=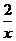 -
- =
=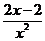 <0
<0
因此,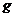 (x)在区间(-1,0)上单调递减,从而
(x)在区间(-1,0)上单调递减,从而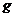 (x)<
(x)<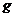 (-1)=-4<0,故当0<
(-1)=-4<0,故当0<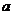 <
<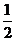 时,
时,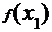 +
+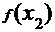 <0
<0
(ii)当0<x<1时,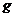 (x)=2inx+
(x)=2inx+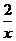 -2,所以
-2,所以
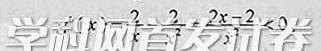
因此。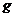 (x)在区间(0,1)上单调递减,从而
(x)在区间(0,1)上单调递减,从而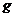 (x)>
(x)>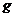 (1)=0.故当
(1)=0.故当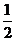 <
<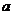 <1时,
<1时,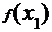 +
+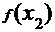 >0
>0
综上所述。满足条件的a的取值范围为(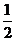 ,1)
,1)
21、(本小题满分13份)
解(I)因为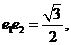 ,所以
,所以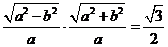 ,即
,即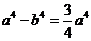 ,因此
,因此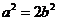 ,从而
,从而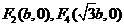 ,于是
,于是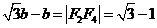 ,所以
,所以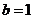 ,
,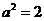 。故
。故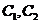 的方程分别为
的方程分别为 ,
,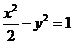 .
.
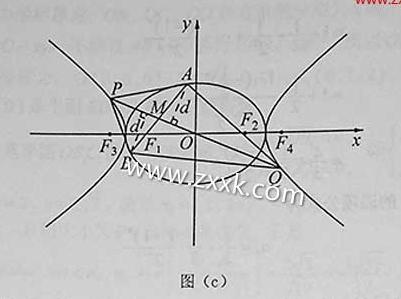
(Ⅱ)因AB不垂直于y轴,且过点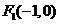 ,故可设直线AB的方程为
,故可设直线AB的方程为
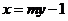 .
.
由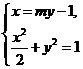 得
得
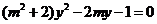
易知此方程的判别式大于0.设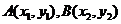 ,则
,则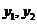 是上述方程的两个实根,所以
是上述方程的两个实根,所以

因此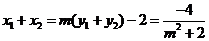 ,于是AB的中点为
,于是AB的中点为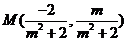 ,故直线PQ的斜率为
,故直线PQ的斜率为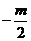 ,PQ的方程为
,PQ的方程为 ,即
,即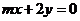 。
。
由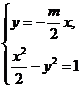 得
得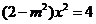 ,所以
,所以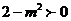 ,且
,且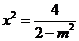 ,
,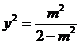 ,从而
,从而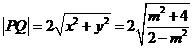 。
。
设点A到直线PQ的距离为d,则点B到直线PQ的距离也为d,所以
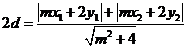 。
。
因为点A、B在直线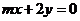 的异侧,所以
的异侧,所以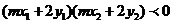 ,于是
,于是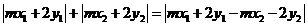 ,
,
从而
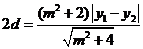
又因为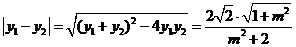 ,所以
,所以
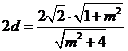 。
。
故四边形APBQ的面积
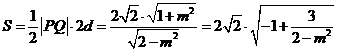 .
.
而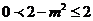 ,故当
,故当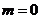 时,S取得最小值2.
时,S取得最小值2.
综上所述,四边形APBQ面积的最小值为2.
20、(本小题满分13份)
解(I)因为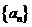 是递增数列,所以
是递增数列,所以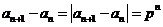 。而
。而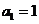 ,因此又
,因此又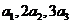 成等差数列,
成等差数列, 解得
解得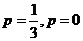
当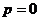 时,
时,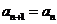 ,这与
,这与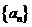 是递增数列矛盾。故
是递增数列矛盾。故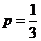 .
.
(Ⅱ)由于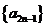 是递增数列,因而
是递增数列,因而 ,于是
,于是
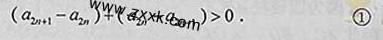
但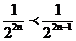 ,所以
,所以
 .
②
.
②
又①,②知,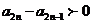 ,因此
,因此
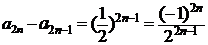 ③
③
因为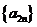 是递减数列,同理可得,
是递减数列,同理可得,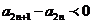 故
故
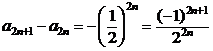 ④
④
由③,④即知,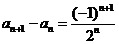 。
。
于是
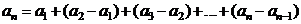
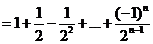
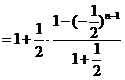
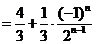 .
.
故数列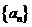 的通项公式为
的通项公式为
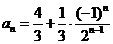
19、(本小题满分12份)
解:(I)如图(a),因为四边形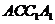 为矩形,所以
为矩形,所以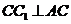 .同理
.同理 。因为
。因为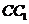 ∥
∥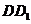 ,所以
,所以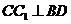 。而
。而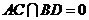 ,因此
,因此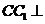 底面ABCD。由题设知,
底面ABCD。由题设知,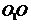 ∥
∥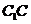 。故
。故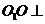 底面ABCD。
底面ABCD。
(Ⅱ)解法I如图(a),过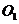 作
作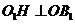 于H,连接
于H,连接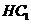 .
.
由(I)知,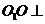 底面ABCD,所以
底面ABCD,所以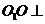 底面
底面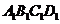 ,于是
,于是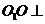
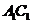 .
.
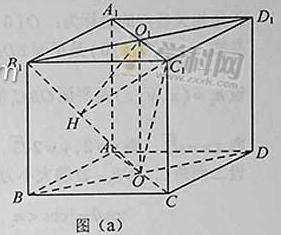
又因为四棱柱ABCD-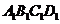 的所有棱长都相等,所以四边形
的所有棱长都相等,所以四边形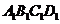 是菱形,因此
是菱形,因此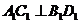 ,从而
,从而 ,所以
,所以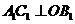 ,于是
,于是 ,进而
,进而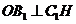 。故
。故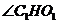 是二面角
是二面角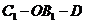 的平面角。
的平面角。
不妨设AB=2。因为 ,所以
,所以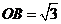 ,
,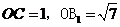 。
。
在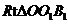 中,易知
中,易知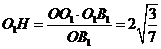 。而
。而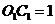 ,
,
于是 。
。
故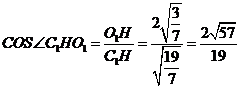 。
。
即二面角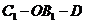 的余弦值为
的余弦值为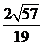 。
。
解法2 因为四棱柱ABCD-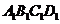 的所有棱长都相等,所以四边形ABCD是菱形,因此
的所有棱长都相等,所以四边形ABCD是菱形,因此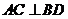 。又
。又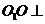 底面ABCD,从而OB,OC,
底面ABCD,从而OB,OC, 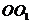 两两垂直。
两两垂直。
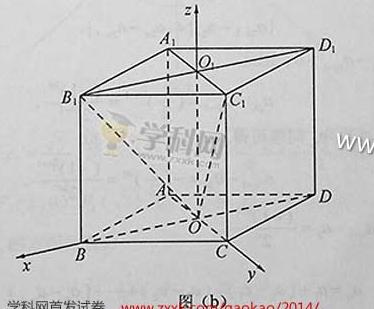
如图(b),以O为坐标原点,OB,OC, 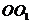 所在直线分别为轴,轴,轴,建立空间直角坐标系。不妨设AB=2.因为
所在直线分别为轴,轴,轴,建立空间直角坐标系。不妨设AB=2.因为 ,所以
,所以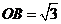 ,
, 于是相关各点的坐标为:O(0,0,0),
于是相关各点的坐标为:O(0,0,0),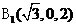 ,
,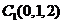 .
.
易知,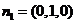 是平面
是平面 的一个法向量。
的一个法向量。
设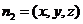 是平面
是平面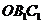 的一个法向量,则
的一个法向量,则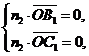 即
即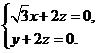 取
取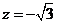 ,则
,则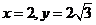 ,所以
,所以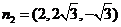 。
。
设二面角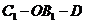 的大小为
的大小为 ,易知
,易知 是锐角,于是
是锐角,于是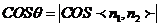
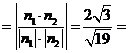
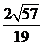 。
。
故二面角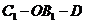 的余弦值为
的余弦值为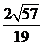
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com